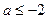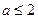题目内容
(本小题15分)
已知函数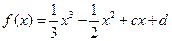 有极值.
有极值.
(1)求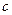 的取值范围;
的取值范围;
(2)若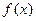 在
在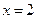 处取得极值,且当
处取得极值,且当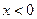 时,
时,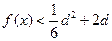 恒成立,求
恒成立,求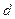 的取值范围.
的取值范围.
已知函数
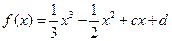 有极值.
有极值.(1)求
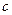 的取值范围;
的取值范围;(2)若
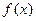 在
在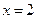 处取得极值,且当
处取得极值,且当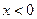 时,
时,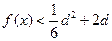 恒成立,求
恒成立,求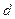 的取值范围.
的取值范围.解:(1)∵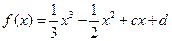 ,∴
,∴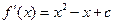 ,
,
要使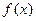 有极值,则方程
有极值,则方程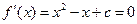 有两个实数解,
有两个实数解,
从而△=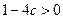 ,∴
,∴ .
.
( 2)∵
2)∵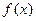 在
在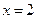 处取得极值,
处取得极值,
∴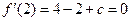 ,
,
∴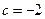 .
.
∴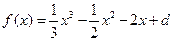 ,
,
∵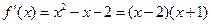 ,
,
∴当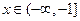 时,
时,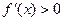 ,函数单调递增,
,函数单调递增,
当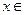
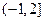 时,
时,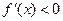 ,函数单调递减.
,函数单调递减.
∴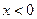 时,
时,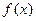 在
在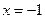 处取得最大值
处取得最大值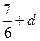 ,
,
∵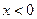 时,
时,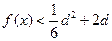 恒成立,
恒成立,
∴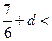
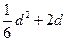 ,即
,即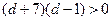 ,
,
∴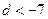 或
或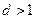 ,即
,即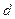 的取值范围是
的取值范围是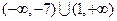 .
.
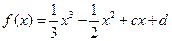 ,∴
,∴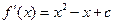 ,
, 要使
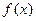 有极值,则方程
有极值,则方程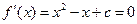 有两个实数解,
有两个实数解,从而△=
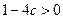 ,∴
,∴ .
. (
 2)∵
2)∵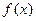 在
在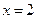 处取得极值,
处取得极值,∴
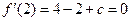 ,
,∴
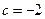 .
. ∴
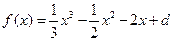 ,
,∵
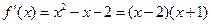 ,
,∴当
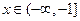 时,
时,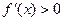 ,函数单调递增,
,函数单调递增,当
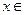
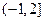 时,
时,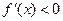 ,函数单调递减.
,函数单调递减.∴
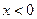 时,
时,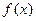 在
在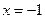 处取得最大值
处取得最大值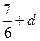 ,
, ∵
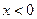 时,
时,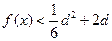 恒成立,
恒成立,∴
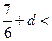
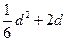 ,即
,即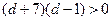 ,
,∴
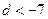 或
或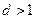 ,即
,即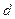 的取值范围是
的取值范围是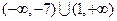 .
.略

练习册系列答案
相关题目
 设函数
设函数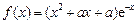 有极值.
有极值. ,试确定
,试确定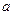 ;
;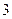 时,只限于
时,只限于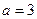 的情况.
的情况.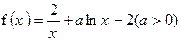
 y=x+2垂直,求函数y=f(x)的单调区间;
y=x+2垂直,求函数y=f(x)的单调区间;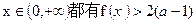 成立,试求a的取值范围;
成立,试求a的取值范围;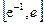 上有两个零点,求实数b的取值范围。
上有两个零点,求实数b的取值范围。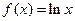 ,
,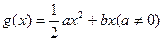
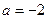 时,函数
时,函数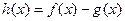 在其定义域内是增函数,求b的取值范围;
在其定义域内是增函数,求b的取值范围;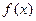 的图象
的图象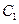 与函数
与函数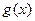 的图象
的图象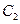 交于点
交于点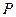 、
、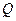 ,过线段
,过线段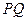 的中点
的中点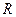 作
作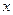 轴的垂线分别交
轴的垂线分别交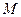 、
、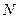 ,问是否存在点
,问是否存在点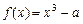 ,x∈[0,+∞).设x1>0,记曲线
,x∈[0,+∞).设x1>0,记曲线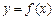 在点M(x1,
在点M(x1,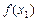 )处的切线为l.
)处的切线为l.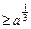 ;②若x1
;②若x1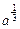 <x2<x1.
<x2<x1.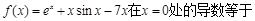
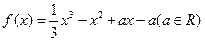 .
.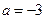 时,求函数
时,求函数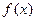 的极值;
的极值;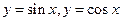 与直线
与直线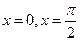 围成区域的面积为 .
围成区域的面积为 .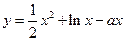 在定义域为增函数,则
在定义域为增函数,则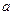 的取值范围是
的取值范围是