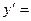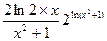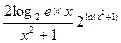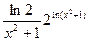题目内容
(本小题满分12分)
设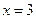 是函数
是函数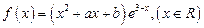 的一个极值点.
的一个极值点.
(1)求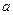 与
与 的关系式(用
的关系式(用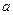 表示
表示 ),并求
),并求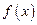 的单调区间;
的单调区间;
(2)设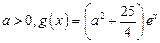 ,若存在
,若存在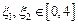 ,使得
,使得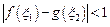 成立,求
成立,求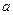 的取值范围.
的取值范围.
设
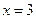 是函数
是函数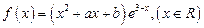 的一个极值点.
的一个极值点.(1)求
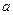 与
与 的关系式(用
的关系式(用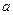 表示
表示 ),并求
),并求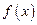 的单调区间;
的单调区间;(2)设
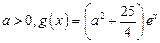 ,若存在
,若存在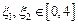 ,使得
,使得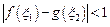 成立,求
成立,求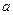 的取值范围.
的取值范围.解:(1)∵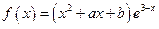
∴
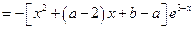 2分
2分
由题意得: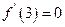 ,即
,即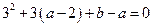
 ,
,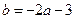 3分
3分
∴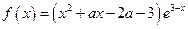 且
且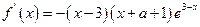
令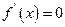 得
得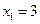 ,
,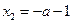
∵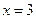 是函数
是函数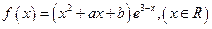 的一个极值点
的一个极值点
∴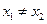 ,即
,即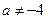
故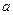 与
与 的关系式为
的关系式为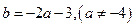 . 4分
. 4分
当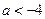 时,
时, ,由
,由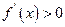 得单增区间为:
得单增区间为: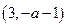 ;
;
由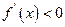 得单减区间为:
得单减区间为: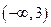 和
和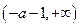 ;
;
当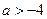 时,
时,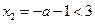 ,由
,由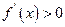 得单增区间为:
得单增区间为: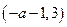 ;
;
由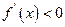 得单减区间为:
得单减区间为: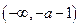 和
和 ; 6分
; 6分
(2)由(1)知:当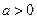 时,
时,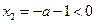 ,
,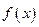 在
在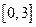 上单调递增,在
上单调递增,在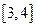 上单调递减,
上单调递减, 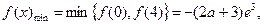
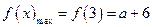 ,
,
∴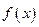 在
在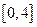 上的值域为
上的值域为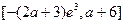 . 8分
. 8分
易知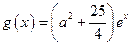 在
在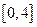 上是增函数,
上是增函数,
∴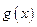 在
在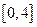 上的值域为
上的值域为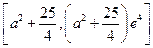 . 10分
. 10分
由于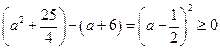 ,
,
又∵要存在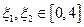 ,使得
,使得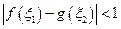 成立,
成立,
∴必须且只须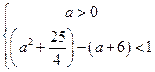 解得:
解得: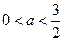 .
.
所以,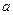 的取值范围为
的取值范围为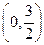 . 12分
. 12分
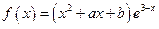
∴

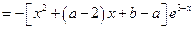 2分
2分由题意得:
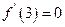 ,即
,即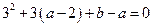
 ,
,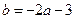 3分
3分∴
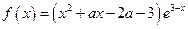 且
且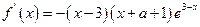
令
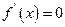 得
得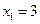 ,
,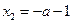
∵
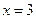 是函数
是函数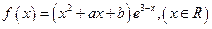 的一个极值点
的一个极值点 ∴
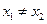 ,即
,即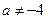
故
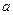 与
与 的关系式为
的关系式为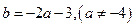 . 4分
. 4分当
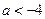 时,
时, ,由
,由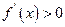 得单增区间为:
得单增区间为: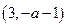 ;
;由
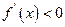 得单减区间为:
得单减区间为: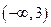 和
和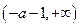 ;
;当
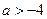 时,
时,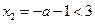 ,由
,由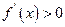 得单增区间为:
得单增区间为: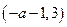 ;
;由
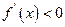 得单减区间为:
得单减区间为: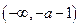 和
和 ; 6分
; 6分(2)由(1)知:当
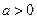 时,
时,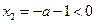 ,
,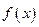 在
在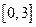 上单调递增,在
上单调递增,在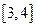 上单调递减,
上单调递减, 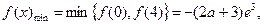
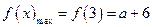 ,
,∴
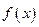 在
在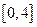 上的值域为
上的值域为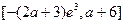 . 8分
. 8分易知
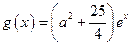 在
在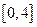 上是增函数,
上是增函数, ∴
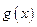 在
在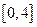 上的值域为
上的值域为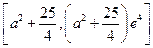 . 10分
. 10分由于
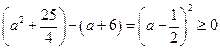 ,
,又∵要存在
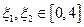 ,使得
,使得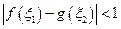 成立,
成立,∴必须且只须
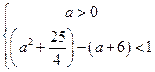 解得:
解得: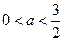 .
. 所以,
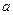 的取值范围为
的取值范围为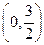 . 12分
. 12分略

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
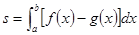 求出的是( )
求出的是( )
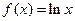 ,
,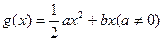
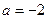 时,函数
时,函数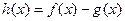 在其定义域内是增函数,求b的取值范围;
在其定义域内是增函数,求b的取值范围;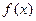 的图象
的图象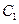 与函数
与函数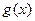 的图象
的图象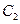 交于点
交于点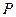 、
、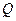 ,过线段
,过线段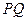 的中点
的中点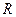 作
作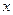 轴的垂线分别交
轴的垂线分别交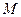 、
、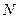 ,问是否存在点
,问是否存在点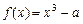 ,x∈[0,+∞).设x1>0,记曲线
,x∈[0,+∞).设x1>0,记曲线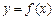 在点M(x1,
在点M(x1,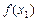 )处的切线为l.
)处的切线为l.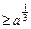 ;②若x1
;②若x1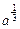 <x2<x1.
<x2<x1.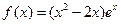 有以下命题:
有以下命题: ;②
;② 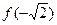 是极小值,
是极小值,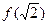 是极大值;
是极大值;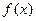 没有最小值,没有最大值; ④
没有最小值,没有最大值; ④ 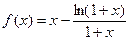
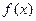
 的最小值
的最小值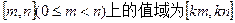 , 试求k的取值范围.
, 试求k的取值范围.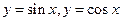 与直线
与直线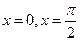 围成区域的面积为 .
围成区域的面积为 .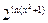 的导数是
的导数是  ( )
( )