题目内容
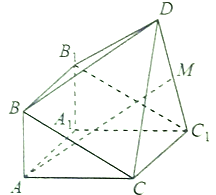
【题目】在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,底面
,底面![]() 是梯形,
是梯形,![]() ∥
∥![]() ,
,![]() ,
,![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)设![]() 为棱
为棱![]() 上一点,
上一点, ![]() ,试确定
,试确定![]() 的值使得二面角
的值使得二面角![]() 为
为![]() .
.
【答案】(1)详见解析(2)![]()
【解析】
试题分析:(1)在梯形ABCD中,过点作B作BH⊥CD于H,通过面面垂直的判定定理即得结论;(2)过点Q作QM∥BC交PB于点M,过点M作MN⊥BD于点N,连QN.则∠QNM是二面角Q-BD-P的平面角,在Rt三角形MNQ中利用tan∠MNQ=QM/MN计算即可
试题解析:(1)证明:∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]()
在梯形![]() 中,过点
中,过点![]() 作
作![]() 于
于![]() ,
,
在![]() 中,
中,![]() ,∴
,∴![]() ,
,
又在![]() 中,
中,![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ……………2分
……………2分
∵![]() .
.
![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
∴![]() 平面
平面![]() ,∵
,∵![]() 平面
平面![]() ,∴
,∴![]() ,……………4分
,……………4分
∴![]() 平面
平面![]() 平面
平面![]() .
.
∴![]() 平面
平面![]() .∵
.∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .……………6分
.……………6分
(1)过点![]() 作
作![]() ∥
∥![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 垂直于
垂直于![]() 于点
于点![]() ,连
,连![]() .
.
由(2)可知![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() ,∵
,∵![]()
∴![]() 平面
平面![]() ,∴
,∴![]() ,
,
∴![]() 是二面角
是二面角![]() 的平面角,∴
的平面角,∴![]() ……………8分
……………8分
∵![]() ,∴
,∴![]() ,
,
∵![]() ∥
∥![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
由(1)知![]() ,∴
,∴![]() ,又∵
,又∵![]()
∵![]() ∥
∥![]() ,∴
,∴![]() ,∴
,∴![]() ……10分
……10分
∵![]() ,∴
,∴![]() ,
,
∴![]() .……………12分
.……………12分

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目