题目内容
(本小题满分12分)已知椭圆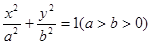 ,离心率为
,离心率为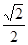 的椭圆经过点
的椭圆经过点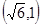 .
.
(1)求该椭圆的标准方程;
(2)过椭圆的一个焦点且互相垂直的直线 分别与椭圆交于
分别与椭圆交于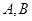 和
和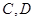 ,是否存在常数
,是否存在常数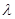 ,使得
,使得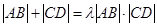 ?若存在,求出实数
?若存在,求出实数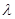 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1)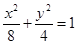 (2)存在实数
(2)存在实数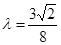 ,使得
,使得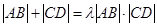 .理由见解析
.理由见解析
解析试题分析:(1)由题可知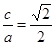 ,即
,即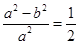 ,
,
由此得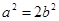 ,故椭圆方程是
,故椭圆方程是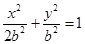 ,
,
将点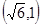 的坐标代入,得
的坐标代入,得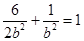 ,解得
,解得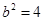 ,
,
故椭圆方程是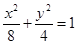 . ……4分
. ……4分
(2)问题等价于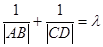 ,即
,即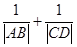 是否是定值问题.
是否是定值问题.
椭圆的焦点坐标是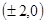 ,不妨取焦点
,不妨取焦点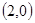 ,
,
当直线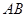 的斜率存在且不等于零时,
的斜率存在且不等于零时,
设直线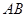 的斜率为
的斜率为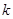 ,则直线
,则直线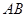 的方程是
的方程是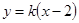 ,
,
代入椭圆方程并整理得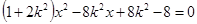
设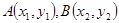 ,则
,则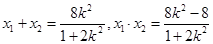 . ……6分
. ……6分
根据弦长公式,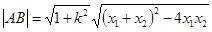 =
=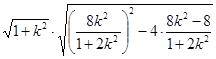
=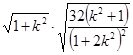 =
=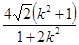 ……8分
……8分
以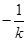 代换
代换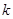 ,得
,得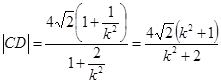 ……9分
……9分
所以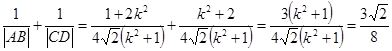
即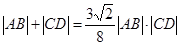 ……10分
……10分
当直线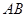 的斜率不存在或等于零时,
的斜率不存在或等于零时,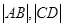 一个是椭圆的长轴长,一个是通径长度,
一个是椭圆的长轴长,一个是通径长度,
此时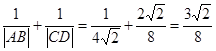 ,即
,即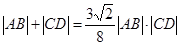 .
.
综上所述,故存在实数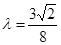 ,使得
,使得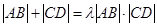 . ……12分
. ……12分
考点:本小题主要考查椭圆标准方程的求解和直线与椭圆的位置关系以及弦长公式的应用,考查学生的转化能力和运算能力.
点评:圆锥曲线问题一般难度较大,要仔细分析,仔细运算,另外设直线方程时,要考虑到直线的斜率是否存在.

练习册系列答案
相关题目
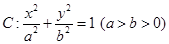 的一个焦点为
的一个焦点为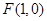 ,点
,点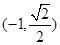 在椭圆
在椭圆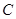 上,点
上,点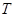 满足
满足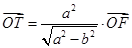 (其中
(其中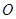 为坐标原点),过点
为坐标原点),过点 作一直线交椭圆于
作一直线交椭圆于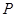 、
、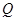 两点 .
两点 .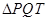 面积的最大值;
面积的最大值;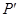 为点
为点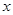 轴的对称点,判断
轴的对称点,判断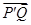 与
与 的位置关系,并说明理由.
的位置关系,并说明理由. ,长轴长为
,长轴长为 ,离心率
,离心率 ,过右焦点
,过右焦点 的直线
的直线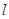 交
交 ,
, 两点:
两点: 的面积;
的面积; 轴的距离少1.
轴的距离少1.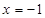 于
于 点,且
点,且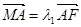 ,
,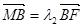 ,
,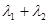 的值。
的值。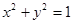 过椭圆
过椭圆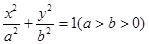 的两焦点,与椭圆有且仅有两个
的两焦点,与椭圆有且仅有两个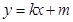 与圆
与圆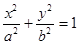 相交于
相交于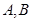 两点记
两点记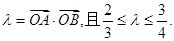
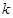 的取值范围;
的取值范围;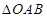 的面积S的取值范围.
的面积S的取值范围. 的离心率为
的离心率为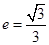 ,以原点为圆心,椭圆短半轴长为半径的圆与直线
,以原点为圆心,椭圆短半轴长为半径的圆与直线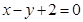 相切,
相切, 分别是椭圆的左右两个顶点,
分别是椭圆的左右两个顶点, 为椭圆
为椭圆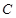 上的动点.
上的动点. 的斜率分别为
的斜率分别为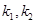 ,求
,求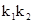 的值。
的值。 是椭圆
是椭圆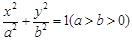 上一点,
上一点,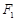 ,
,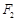 是椭圆的两焦点,且满足
是椭圆的两焦点,且满足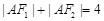
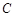 、
、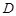 是椭圆上任两点,且直线
是椭圆上任两点,且直线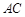 、
、 的斜率分别为
的斜率分别为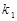 、
、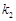 ,若存在常数
,若存在常数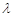 使
使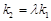 ,求直线
,求直线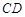 的斜率.
的斜率. 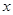 轴上,左右焦点分别为
轴上,左右焦点分别为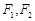 ,且
,且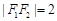 ,
,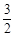 )在椭圆C上.
)在椭圆C上.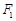 的直线
的直线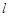 与椭圆
与椭圆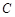 相交于
相交于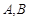 两点,且
两点,且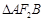 的面积为
的面积为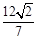 ,求直线
,求直线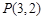 ,焦点在坐标轴上,长轴长是短轴长的3倍,求该椭圆的方程.
,焦点在坐标轴上,长轴长是短轴长的3倍,求该椭圆的方程.