题目内容
9.若圆C:x2+y2-2x-4y+m=0与直线x+2y-4=0相交于M、N两点,且|MN|=$\frac{{4\sqrt{5}}}{5}$(1)求m的值;
(2)是否存在直线l:x-2y+c=0,使得圆上有四点到直线l的距离为$\frac{{\sqrt{5}}}{5}$,若存在,求出c的取值范围,若不存在,说明理由.
分析 (1)利用点到直线的距离可得:圆心(1,2)到直线l的距离d,利用$(\frac{2\sqrt{5}}{5})^{2}+(\frac{1}{\sqrt{5}})^{2}$=5-m,即可解得m.
(2)如图所示,圆心(1,2)到直线l的距离d=$\frac{|c-3|}{\sqrt{5}}$,假设存在直线l:x-2y+c=0,使得圆上有四点到直线l的距离为$\frac{\sqrt{5}}{5}$,必须满足1-$\frac{|c-3|}{\sqrt{5}}$>$\frac{\sqrt{5}}{5}$,解出即可.
解答 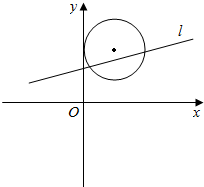 解:(1)由方程C:x2+y2-2x-4y+m=0变为(x-1)2+(y-2)2=5-m.
解:(1)由方程C:x2+y2-2x-4y+m=0变为(x-1)2+(y-2)2=5-m.
圆心(1,2)到直线l的距离d=$\frac{|1+4-4|}{\sqrt{5}}$=$\frac{1}{\sqrt{5}}$,
∵弦长|MN|=$\frac{{4\sqrt{5}}}{5}$,
∴$(\frac{2\sqrt{5}}{5})^{2}+(\frac{1}{\sqrt{5}})^{2}$=5-m,解得m=4.
故m=4.
(2)如图所示,圆心(1,2)到直线l的距离d=$\frac{|1-4+c|}{\sqrt{5}}$=$\frac{|c-3|}{\sqrt{5}}$,
假设存在直线l:x-2y+c=0,使得圆上有四点到直线l的距离为$\frac{\sqrt{5}}{5}$,
必须1-$\frac{|c-3|}{\sqrt{5}}$>$\frac{\sqrt{5}}{5}$,
解得4-$\sqrt{5}$<c<2+$\sqrt{5}$.
因此存在c∈(4-$\sqrt{5}$,2+$\sqrt{5}$),满足条件.
点评 本题考查了直线与圆的位置关系、弦长公式、勾股定理等基础知识与基本技能方法,属于中档题.

| A. | (-∞,-1) | B. | $({-1,-\frac{2}{3}})$ | C. | $({-\frac{2}{3},3})$ | D. | (3,+∞) |
| A. | V1>V2 | B. | V1<V2 | ||
| C. | V1=V2 | D. | V1,V2无明确大小关系 |
| A. | 12 | B. | 10 | C. | 8 | D. | 25 |
| A. | [-1,0] | B. | [-1,1) | C. | (-∞,0] | D. | [-1,+∞) |