题目内容
19．已知|$\overrightarrow{a}$|=2$\sqrt{3}$，|$\overrightarrow{b}$|=6，$\overrightarrow{a}$•$\overrightarrow{b}$=-18，则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角θ是150°．分析 把已知数据代入向量的夹角公式可得夹角的余弦值，可得夹角．
解答 解：∵|$\overrightarrow{a}$|=2$\sqrt{3}$，|$\overrightarrow{b}$|=6，$\overrightarrow{a}$•$\overrightarrow{b}$=-18，
∴cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{-18}{2\sqrt{3}×6}$=-$\frac{\sqrt{3}}{2}$，
∴θ=150°
故答案为：150°
点评 本题考查向量的夹角公式，属基础题．
练习册系列答案
相关题目
10．函数f（x）=-3x在区间[1，2]上的最小值是（ ）
| A． | -9 | B． | -6 | C． | -3 | D． | -$\frac{1}{3}$ |
7．
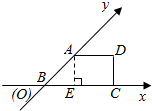有一块多边形的菜地它的水平放置的平面图形的斜二测直观图是直角梯形，如图所示∠ABC=45°AB=2，AD=1，DC⊥BC，则这块菜地的面积为．（ ）
有一块多边形的菜地它的水平放置的平面图形的斜二测直观图是直角梯形，如图所示∠ABC=45°AB=2，AD=1，DC⊥BC，则这块菜地的面积为．（ ）| A． | 2+2$\sqrt{2}$ | B． | 4+2$\sqrt{2}$ | C． | 1+$\sqrt{2}$ | D． | 1+$\sqrt{2}$ |
14．从含有8个个体的总体中抽取一个容量为4的样本，则总体中每个个体被抽到的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{4}$ |
4．抛掷两颗均匀的正方体骰子，所得的两个点数中一个恰是另一个的两倍的概率是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{6}$ | C． | $\frac{1}{8}$ | D． | $\frac{1}{12}$ |
11．甲，乙两人进行射击比赛，每人射击6次，他们命中的环数如下表：
（Ⅰ）根据上表中的数据，判断甲，乙两人谁发挥较稳定；
（Ⅱ）把甲6次射击命中的环数看成一个总体，用简单随机抽样方法从中抽取两次命中的环数组成一个样本，求该样本平均数与总体平均数之差的绝对值不超过0.5的概率．
注：$\overline{x}$=$\frac{1}{n}$（x1+x2+…+xn）
S2=$\frac{1}{n}$[（x1-$\overline{x}$）2+（x2-$\overline{x}$）2+…+（xn-$\overline{x}$）2]．
| 甲 | 5 | 8 | 7 | 9 | 10 | 6 |
| 乙 | 6 | 7 | 4 | 10 | 9 | 9 |
（Ⅱ）把甲6次射击命中的环数看成一个总体，用简单随机抽样方法从中抽取两次命中的环数组成一个样本，求该样本平均数与总体平均数之差的绝对值不超过0.5的概率．
注：$\overline{x}$=$\frac{1}{n}$（x1+x2+…+xn）
S2=$\frac{1}{n}$[（x1-$\overline{x}$）2+（x2-$\overline{x}$）2+…+（xn-$\overline{x}$）2]．
8．在对人们的休闲方式的一次调查中，共调查了124人，其中女性70人，男性54人．女性中有43人主要的休闲方式是看电视，另外27人主要的休闲方式是运动；男性中有21人主要的休闲方式是看电视，另外33人主要的休闲方式是运动．
（Ⅰ）根据以上数据建立一个2×2的列联表；
（Ⅱ）判断性别与休闲方式是否有关系？
本题参考：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+c）（b+d）（a+b）（c+d）}$．
（Ⅰ）根据以上数据建立一个2×2的列联表；
（Ⅱ）判断性别与休闲方式是否有关系？
| P（k2＞k） | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 3.84 | 5.024 | 6.635 | 7.879 |