题目内容
17.四条曲线x2=2y,x=2,x=-2,y=0围成的封闭图形绕y轴旋转一周所得的旋转体的体积为V1:满足$\left\{\begin{array}{l}y≥0\\{x^2}+{({y-1})^2}≤1\\{x^2}+{y^2}≤4\end{array}\right.$的平面区域绕y轴旋转一周所得的旋转体的体积为V2,则( )| A. | V1>V2 | B. | V1<V2 | ||
| C. | V1=V2 | D. | V1,V2无明确大小关系 |
分析 分别求出两个旋转体的体积进行比较即可.
解答 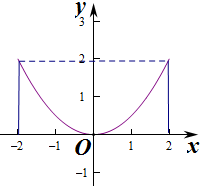
 解:第一个旋转体的体积为π×22×2-${∫}_{-2}^{2}$π($\frac{{x}^{2}}{2}$)2dx
解:第一个旋转体的体积为π×22×2-${∫}_{-2}^{2}$π($\frac{{x}^{2}}{2}$)2dx
=8π-$\frac{π}{4}$${∫}_{-2}^{2}$x4dx
=8π-$\frac{π}{4}$×$\frac{1}{5}{x}^{5}$|${\;}_{-2}^{2}$
=8π-$\frac{π}{4}$×$\frac{64}{5}$
=8$π-\frac{16π}{5}$=$\frac{24π}{5}$,
第二个旋转体的体积为半径为1的球,体积V2=$\frac{4}{3}•π×{1}^{3}$=$\frac{4π}{3}$.
则V1>V2,
故选:A
点评 本题主要考查旋转体的体积的大小比较,考察学生的计算能力.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
7.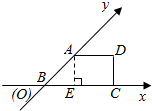 有一块多边形的菜地它的水平放置的平面图形的斜二测直观图是直角梯形,如图所示∠ABC=45°AB=2,AD=1,DC⊥BC,则这块菜地的面积为.( )
有一块多边形的菜地它的水平放置的平面图形的斜二测直观图是直角梯形,如图所示∠ABC=45°AB=2,AD=1,DC⊥BC,则这块菜地的面积为.( )
 有一块多边形的菜地它的水平放置的平面图形的斜二测直观图是直角梯形,如图所示∠ABC=45°AB=2,AD=1,DC⊥BC,则这块菜地的面积为.( )
有一块多边形的菜地它的水平放置的平面图形的斜二测直观图是直角梯形,如图所示∠ABC=45°AB=2,AD=1,DC⊥BC,则这块菜地的面积为.( )| A. | 2+2$\sqrt{2}$ | B. | 4+2$\sqrt{2}$ | C. | 1+$\sqrt{2}$ | D. | 1+$\sqrt{2}$ |
8.在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(Ⅰ)根据以上数据建立一个2×2的列联表;
(Ⅱ)判断性别与休闲方式是否有关系?
本题参考:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+c)(b+d)(a+b)(c+d)}$.
(Ⅰ)根据以上数据建立一个2×2的列联表;
(Ⅱ)判断性别与休闲方式是否有关系?
| P(k2>k) | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 3.84 | 5.024 | 6.635 | 7.879 |
6.设P(1,f(1))是曲线C:f(x)=x2+2x+3上的一点,则曲线C过点P的切线方程是( )
| A. | 4x-y+10=0 | B. | 4x-y+2=0 | C. | x-4y+10=0 | D. | x-4y+2=0 |