题目内容
12.给出下列命题①函数y=sinx的图象对称中心为点(kπ,0)(k∈Z)
②若向量a,b,c满足$\overrightarrow{a}$$•\overrightarrow{b}$=$\overrightarrow{a}$$•\overrightarrow{c}$,且$\overrightarrow{a}$$≠\overrightarrow{0}$,则$\overrightarrow{b}$$≠\overrightarrow{c}$
③将函数y=2sin(2x+$\frac{π}{3}$)的图象向右平移$\frac{π}{6}$个单位得到y=2xin2x的图象
④若an=an+1(n∈N*),则数列{an}既是等差数列又是等比数列
其中正确命题的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据正弦函数的对称性,可判断①;根据向量数量积的定义,可判断②;根据函数图象的平移变换法则,可判断③;根据等差,等比数列的定义,可判断④.
解答 解:①函数y=sinx的图象对称中心为点(kπ,0)(k∈Z),故①正确;
②若向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足$\overrightarrow{a}$$•\overrightarrow{b}$=$\overrightarrow{a}$$•\overrightarrow{c}$,且$\overrightarrow{a}$≠$\overrightarrow{0}$,则$\overrightarrow{b}$,$\overrightarrow{c}$在向量$\overrightarrow{a}$上的投影相等,但$\overrightarrow{b}$=$\overrightarrow{c}$不一定成立,故②错误;
③将函数y=2sin(2x+$\frac{π}{3}$)的图象向右平移$\frac{π}{6}$个单位得到y=2sin[2(x-$\frac{π}{6}$)+$\frac{π}{3}$]=2xin2x的图象,故③正确;
④若an=an+1=0,(n∈N*),则数列{an}是等差数列,但不是等比数列,故④错误;
故正确的命题的个数为2个,
故选:B
点评 本题考查的知识点是命题的真假判断与应用,此类题型往往综合较多的其它知识点,综合性强,难度中档.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
17.下列说法正确的是( )
| A. | 若命题p,¬q都是真命题,则命题“¬p∧¬q”为真命题 | |
| B. | “x=1”是“x2+2x-3=0”的必要不充分条件 | |
| C. | 命题“?x∈R,f(x)>0”的否定是“?x0∈R,f(x0)<0” | |
| D. | 命题“若xy=0,则x=0或y=0”的逆否命题为真命题 |
2.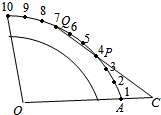 某转弯路段为四分之一圆环,圆环道路外侧均匀栽种了10棵树(如图所示),小李在半径OA的延长线上一点C处观察到第四棵树(P点),第七棵树(Q点)与点C在同一条直线上,并测得AC=100米,则此弧形道路的大圆半径OA的长为( )
某转弯路段为四分之一圆环,圆环道路外侧均匀栽种了10棵树(如图所示),小李在半径OA的延长线上一点C处观察到第四棵树(P点),第七棵树(Q点)与点C在同一条直线上,并测得AC=100米,则此弧形道路的大圆半径OA的长为( )
 某转弯路段为四分之一圆环,圆环道路外侧均匀栽种了10棵树(如图所示),小李在半径OA的延长线上一点C处观察到第四棵树(P点),第七棵树(Q点)与点C在同一条直线上,并测得AC=100米,则此弧形道路的大圆半径OA的长为( )
某转弯路段为四分之一圆环,圆环道路外侧均匀栽种了10棵树(如图所示),小李在半径OA的延长线上一点C处观察到第四棵树(P点),第七棵树(Q点)与点C在同一条直线上,并测得AC=100米,则此弧形道路的大圆半径OA的长为( )| A. | 100$\sqrt{3}$米 | B. | 100($\sqrt{3}$+1)米 | C. | 200米 | D. | 100($\sqrt{3}$+$\sqrt{2}$)米 |