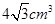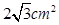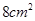题目内容
在空间四边形 中,
中,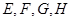 分别是
分别是 的中点。若
的中点。若 ,且
,且 与
与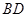 所成的角为
所成的角为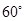 ,则四边形
,则四边形 的面积为( )
的面积为( )
A. | B. | C. | D.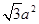 |
A
解析试题分析:连接EH,因为EH是△ABD的中位线,所以EH∥BD,且EH=BD.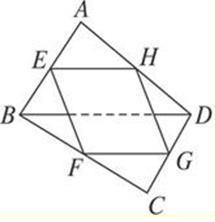
同理,FG∥BD,EF∥AC,且FG=BD,EF=AC.
所以EH∥FG,且EH=FG.
所以四边形EFGH为平行四边形.
因为AC=BD=a,AC与BD所成的角为60°
所以EF=EH.所以四边形EFGH为菱形,∠EFG=60°.
∴四边形EFGH的面积是2×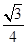 ×(
×(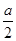 )2=
)2=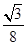 a2
a2
故答案为: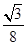 a2选A.
a2选A.
考点:本题主要是考查的知识点简单几何体和公理四,公理四:和同一条直线平行的直线平行,证明菱形常用方法是先证明它是平行四边形再证明邻边相等相等,以及面积公式属于基础题.
点评:解决该试题的关键是先证明四边形EFGH为菱形,然后说明∠EFG=60°,最后根据三角形的面积公式即可求出所求.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知球的半径为2,相互垂直的两个平面分别截球面得两个圆.若两圆的公共弦长为2,则两圆的圆心距等于( )
| A.1 | B. | C. | D.2 |
( )球的表面积与它的内接正方体的表面积之比是
A.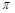 | B.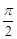 | C.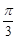 | D.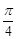 |
设四棱锥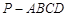 的底面不是平行四边形,用平面
的底面不是平行四边形,用平面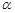 去截此四棱锥,使得截面是平行四边形,则这样的平面
去截此四棱锥,使得截面是平行四边形,则这样的平面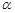 ( )
( )
| A.不存在 | B.有且只有1个 | C.恰好有4个 | D.有无数多个 |




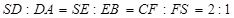 ,若仍用该容器盛水,最多盛水(可以任意情形放置)为原三棱锥体积的( )
,若仍用该容器盛水,最多盛水(可以任意情形放置)为原三棱锥体积的( )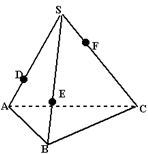
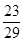
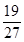
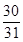
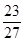
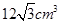 ,其三视图中的俯视图如图所示,则其侧(左)视图的面积是( )
,其三视图中的俯视图如图所示,则其侧(左)视图的面积是( )