题目内容
设四棱锥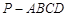 的底面不是平行四边形,用平面
的底面不是平行四边形,用平面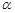 去截此四棱锥,使得截面是平行四边形,则这样的平面
去截此四棱锥,使得截面是平行四边形,则这样的平面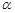 ( )
( )
| A.不存在 | B.有且只有1个 | C.恰好有4个 | D.有无数多个 |
D
解析试题分析:设四棱锥的两组不相邻的侧面的交线为m,n,直线m、n确定了平面β,作与β平行的平面α与四棱锥侧棱相截,则截得的四边形是平行四边形.这样的平面α有无数多个.
故选D.
考点:线面平行的判定定理;线面平行的性质定理。
点评:做此题的关键是确定平面β,考查了学生的空间想象能力。属于中档题。

练习册系列答案
相关题目
右图是底面半径为1,母线长均为2的圆锥和圆柱的组合体,则该组合体的侧视图的面积为( )
A.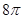 | B.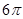 | C.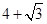 | D.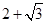 |
如图,四棱锥S—ABCD的底面为正方形,SD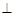 底面ABCD,则下列结论中不正确的是
底面ABCD,则下列结论中不正确的是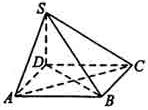
| A.AC⊥SB |
| B.AB∥平面SCD |
| C.SA与平面SBD所成的角等于SC与平面SBD所成的角 |
| D.AB与SC所成的角等于DC与SA所成的角 |
在空间四边形 中,
中,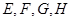 分别是
分别是 的中点。若
的中点。若 ,且
,且 与
与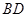 所成的角为
所成的角为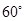 ,则四边形
,则四边形 的面积为( )
的面积为( )
A. | B. | C. | D.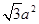 |
如图⑴、⑵、⑶、⑷为四个几何体的三视图,根据三视图可以判断这四个几何体依次分别为
| A.三棱台、三棱柱、圆锥、圆台 | B.三棱台、三棱锥、圆锥、圆台 |
| C.三棱柱、正四棱锥、圆锥、圆台 | D.三棱柱、三棱台、圆锥、圆台 |
三棱锥的三条侧棱两两垂直,其长分别是1、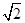 、
、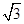 ,则此三棱锥的外接球的表面积是( )
,则此三棱锥的外接球的表面积是( )
| A.6π | B.5π | C.4π | D.9π |
正方体的内切球,与各棱相切的球,外接球的体积之比为( )
| A.1:2:3 | B.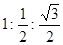 | C.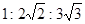 | D.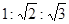 |
下列几何体中是旋转体的是
①圆柱;②六棱锥;③正方体;④球体;⑤四面体.
| A.①和⑤ | B.① | C.③和④ | D.①和④ |


