题目内容
把正方形ABCD沿对角线AC折起,当以A、B、C、D四点为顶点的棱锥体积最大时,直线BD和平面ABC所成的角的大小为 ( )
A. 90° B .60° C . 45° D .30°
C
解析试题分析:三棱锥 体积最大时平面
体积最大时平面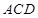
 平面
平面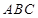 ,取
,取 边中点
边中点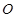 ,连接
,连接 ,
,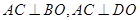 ,
, ,BD和平面ABC所成的角为
,BD和平面ABC所成的角为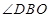 ,
,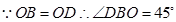
考点:直线与平面所成角
点评:本题先由体积最大得到两面垂直,进而转化为线面垂直找到所求角

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
一个几何体的三视图如图所示,则该几何体的表面积
| A.38-π | B.38 | C.38+π | D.38-2π |
如图,四棱锥S—ABCD的底面为正方形,SD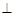 底面ABCD,则下列结论中不正确的是
底面ABCD,则下列结论中不正确的是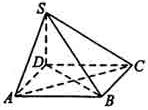
| A.AC⊥SB |
| B.AB∥平面SCD |
| C.SA与平面SBD所成的角等于SC与平面SBD所成的角 |
| D.AB与SC所成的角等于DC与SA所成的角 |
在空间四边形 中,
中,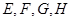 分别是
分别是 的中点。若
的中点。若 ,且
,且 与
与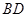 所成的角为
所成的角为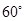 ,则四边形
,则四边形 的面积为( )
的面积为( )
A. | B. | C. | D.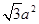 |
如图⑴、⑵、⑶、⑷为四个几何体的三视图,根据三视图可以判断这四个几何体依次分别为
| A.三棱台、三棱柱、圆锥、圆台 | B.三棱台、三棱锥、圆锥、圆台 |
| C.三棱柱、正四棱锥、圆锥、圆台 | D.三棱柱、三棱台、圆锥、圆台 |
正方体的内切球,与各棱相切的球,外接球的体积之比为( )
| A.1:2:3 | B.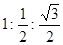 | C.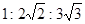 | D.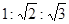 |
某几何体的三视图如图所示,则该几何体的体积是( )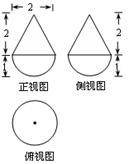
A. | B.2? | C.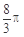 | D. |
 是边长为
是边长为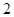 的正三角形,俯视图为正六边形,那么该几何体的左视图的面积为
的正三角形,俯视图为正六边形,那么该几何体的左视图的面积为 
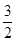
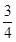

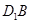 所成角的余弦值为()
所成角的余弦值为()