题目内容
若定义在R上的偶函数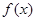 满足
满足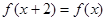 ,且当
,且当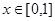 时,
时,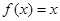 ,则函数
,则函数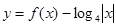 的零点的个数为( )
的零点的个数为( )
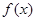 满足
满足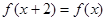 ,且当
,且当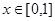 时,
时,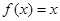 ,则函数
,则函数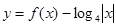 的零点的个数为( )
的零点的个数为( )| A.4 | B.5 | C.6 | D.8 |
C
因为由题意知,函数y=f(x)是个周期为2的周期函数,且是个偶函数,在一个周期[-1,1)上,
图象是2条斜率分别为1和-1的线段,且 0≤f(x)≤1,同理得到在其他周期上的图象.
函数y=log4|x|也是个偶函数,先看他们在[0,+∞)上的交点个数,则它们总的交点个数是在[0,+∞)
上的交点个数的2倍,在(0,+∞)上,y=log4|x|=log4x,图象过(1,0),和(4,1),是单调增函数,与f(x)交与3个不同点,∴函数y=f(x)的图象与函数y=log4|x|的图象的交点个数是6个.
故选C.
图象是2条斜率分别为1和-1的线段,且 0≤f(x)≤1,同理得到在其他周期上的图象.
函数y=log4|x|也是个偶函数,先看他们在[0,+∞)上的交点个数,则它们总的交点个数是在[0,+∞)
上的交点个数的2倍,在(0,+∞)上,y=log4|x|=log4x,图象过(1,0),和(4,1),是单调增函数,与f(x)交与3个不同点,∴函数y=f(x)的图象与函数y=log4|x|的图象的交点个数是6个.
故选C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
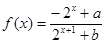 (
(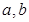 为实常数).
为实常数).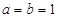 时,证明:
时,证明: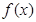 不是奇函数;
不是奇函数;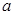 与
与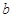 的值;
的值;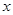 、c都有
、c都有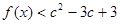 成立
成立 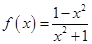 ,则有( )
,则有( )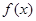 是奇函数,
是奇函数,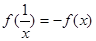
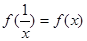
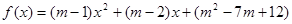 为偶函数,则
为偶函数,则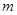 =( )
=( )
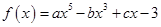 ,
,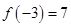 ,则
,则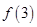 的值为 ___________
的值为 ___________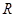 上的函数
上的函数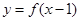 的图像关于
的图像关于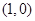 对称,且当
对称,且当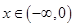 时,
时,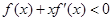 (其中
(其中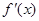 是
是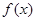 的导函数),若
的导函数),若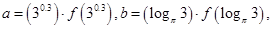
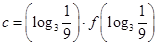 ,则
,则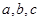 的大小关系是( )
的大小关系是( )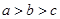
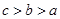
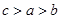
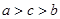
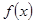 是定义在
是定义在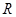 上的奇函数,当
上的奇函数,当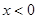 时,
时,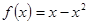 ,则当
,则当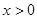 时,
时,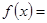 ( )
( )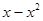
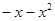
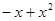
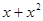
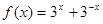 与
与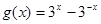 的定义域均为R,则
的定义域均为R,则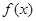 与
与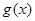 与均为偶函数 B.
与均为偶函数 B.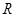 上的偶函数
上的偶函数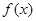 满足
满足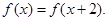 当
当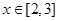 时,
时,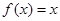 ,则
,则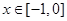 时,
时,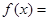 ________.
________.