题目内容
【题目】某城市有一直角梯形绿地![]() ,其中
,其中![]() ,
,![]() km,
km,![]() km.现过边界
km.现过边界![]() 上的点
上的点![]() 处铺设一条直的灌溉水管
处铺设一条直的灌溉水管![]() ,将绿地分成面积相等的两部分.
,将绿地分成面积相等的两部分.
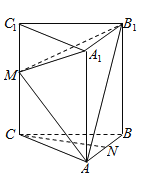
(1)如图①,若![]() 为
为![]() 的中点,
的中点,![]() 在边界
在边界![]() 上,求灌溉水管
上,求灌溉水管![]() 的长度;
的长度;
(2)如图②,若![]() 在边界
在边界![]() 上,求灌溉水管
上,求灌溉水管![]() 的最短长度.
的最短长度.

【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:(1)由面积相等建立等量关系:先确定直角梯形高![]() ,求得直角梯形
,求得直角梯形![]() 面积
面积![]() ,再表示四边形
,再表示四边形![]() 的面积:分割成一个小直角梯形
的面积:分割成一个小直角梯形![]() 及一个直角三角形
及一个直角三角形![]() ,其中
,其中![]() 为
为![]() 中点,根据四边形
中点,根据四边形![]() 的面积为直角梯形
的面积为直角梯形![]() 面积一半,可解得
面积一半,可解得![]() ,进而求得
,进而求得![]() (2)易得
(2)易得![]() ,进而可得
,进而可得![]() ,其中
,其中![]() ,
,![]() ,根据
,根据![]() 的面积为直角梯形
的面积为直角梯形![]() 面积一半,可解得
面积一半,可解得![]() ,再由余弦定理可得
,再由余弦定理可得![]() ,利用基本不等式求最值
,利用基本不等式求最值
试题解析:(1)因为![]() ,
,![]() ,
,![]() ,
,
所以![]() ,……………………………………2分
,……………………………………2分
取![]() 中点
中点![]() ,
,
则四边形![]() 的面积为
的面积为![]() ,
,
即![]()
![]() ,
,
解得![]() ,…………………………………………6分
,…………………………………………6分
所以![]() (km).
(km).
故灌溉水管![]() 的长度为
的长度为![]() km.……………………8分
km.……………………8分
(2)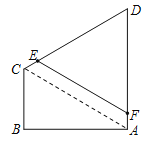
设![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,
,
所以在![]() 中,
中,![]() ,
,
所以![]() ,
,
所以![]() 的面积为
的面积为![]() ,
,
又![]() ,所以
,所以![]() ,即
,即![]() .……………………12分
.……………………12分
在![]() 中,由余弦定理,得
中,由余弦定理,得![]() ,
,
当且仅当![]() 时,取“
时,取“![]() ”.
”.
故灌溉水管![]() 的最短长度为
的最短长度为![]() km.……………………………………16分
km.……………………………………16分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目