题目内容
【题目】已知函数![]() 则x∈[﹣1,e]时,f(x)的最小值为_____;设g(x)=[f(x)]2﹣f(x)+a若函数g(x)有6个零点,则实数a的取值范围是_____.
则x∈[﹣1,e]时,f(x)的最小值为_____;设g(x)=[f(x)]2﹣f(x)+a若函数g(x)有6个零点,则实数a的取值范围是_____.
【答案】﹣4 (0,![]() )
)
【解析】
根据各段函数的单调性分别求出各段的最小值或者下确界,即可求出![]() ,
,![]() 时,
时,![]() 的最小值;
的最小值;
令![]() ,根据题意再结合函数
,根据题意再结合函数![]() 的图象,以及
的图象,以及![]() 的图象即可求出实数
的图象即可求出实数![]() 的取值范围.
的取值范围.
解:当![]() ,
,![]() 时,
时,![]() ,此时函数在区间上单调递增,故此时函数最小值为
,此时函数在区间上单调递增,故此时函数最小值为![]() ,
,
当![]() ,
,![]() 时,
时,![]() ,则
,则![]() 时,
时,![]() (舍
(舍![]() 或0,
或0,
且有![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
因为![]() ,
,
故函数![]() 在
在![]() ,
,![]() 上的最小值为
上的最小值为![]() ;
;
令![]() ,
,![]() 即
即![]() ,
,
作出函数![]() 的图象,如图所示:
的图象,如图所示:
直线![]() 与函数
与函数![]() 的图象最多只有三个交点,所以
的图象最多只有三个交点,所以![]() ,
,
即说明方程![]() 有两个
有两个![]() 内的不等根,
内的不等根,
亦即函数![]() 在
在![]() 内的图象与直线
内的图象与直线![]() 有两个交点,
有两个交点,
因为![]() ,根据
,根据![]() 的图象可知,
的图象可知,![]() ,
,
即实数![]() 的取值范围为
的取值范围为![]() .
.
故答案为:![]() ;
;![]() .
.
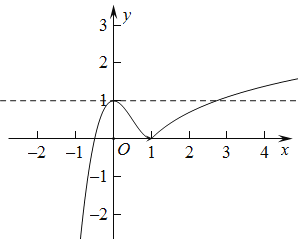

练习册系列答案
相关题目