题目内容
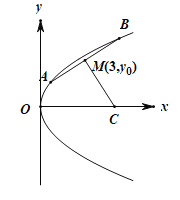
【题目】已知点F1、F2分别为双曲线C：
（a＞0，b＞0）的左、右焦点，点M（x0，y0）（x0＜0）为C的渐近线与圆x2+y2＝a2的一个交点，O为坐标原点，若直线F1M与C的右支交于点N，且|MN|＝|NF2|+|OF2|，则双曲线C的离心率为_____．
【答案】
【解析】
由题意画出图形，可得直线F1M与圆O相切于点M，且|MF1|＝b，再由双曲线的定义隐含条件列式求解双曲线的离心率．
如图所示：
由题意可得，直线F1M与圆O相切于点M，且|MF1|＝b，
由双曲线的定义可知，2a＝|NF1|﹣|NF2|＝|MN|+|MF1|﹣|NF2|，
∵|MN|＝|NF2|+|OF2|，且|OF2|＝c，
∴2a＝b+c，即b＝2a﹣c，
∴b2＝（2a﹣c）2＝c2﹣4ac+4a2，
又b2＝c2﹣a2，
联立解得4c＝5a，即e
．
故答案为：
．
练习册系列答案
口算能手系列答案
相关题目
