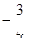题目内容
(、(本题16分)
如图,有一块抛物线形状的钢板,计划将此钢板切割成等腰梯形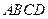 的形状,使得
的形状,使得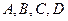 都落在抛物线上,点
都落在抛物线上,点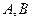 关于抛物线的轴对称,且
关于抛物线的轴对称,且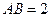 ,抛物线的顶点到底边的距离是
,抛物线的顶点到底边的距离是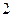 ,记
,记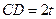 ,梯形面积为
,梯形面积为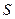 .
.
(1)以抛物线的顶点为坐标原点,其对称轴为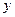 轴建立坐标系,使抛物线开口向下,求出该抛物线的方程;
轴建立坐标系,使抛物线开口向下,求出该抛物线的方程;
(2)求面积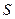 关于
关于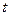 的函数解析式,并写出其定义域;
的函数解析式,并写出其定义域;
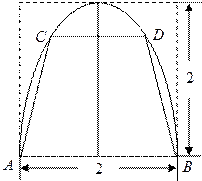 (3)求面积
(3)求面积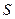 的最大值.
的最大值.
如图,有一块抛物线形状的钢板,计划将此钢板切割成等腰梯形
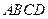 的形状,使得
的形状,使得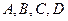 都落在抛物线上,点
都落在抛物线上,点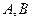 关于抛物线的轴对称,且
关于抛物线的轴对称,且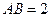 ,抛物线的顶点到底边的距离是
,抛物线的顶点到底边的距离是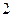 ,记
,记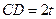 ,梯形面积为
,梯形面积为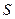 .
.(1)以抛物线的顶点为坐标原点,其对称轴为
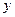 轴建立坐标系,使抛物线开口向下,求出该抛物线的方程;
轴建立坐标系,使抛物线开口向下,求出该抛物线的方程;(2)求面积
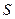 关于
关于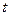 的函数解析式,并写出其定义域;
的函数解析式,并写出其定义域;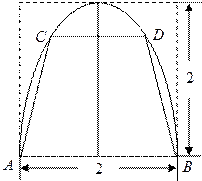 (3)求面积
(3)求面积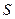 的最大值.
的最大值.解(1)以抛物线的顶点为坐标原点,其对称轴为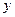 轴建立坐标系,
轴建立坐标系,
设抛物线方程为: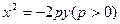 ,
,
由图得抛物线过点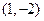 ,代入
,代入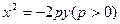 求得
求得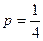 ,
,
所以外轮廓线所在抛物线的方程: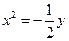 ………………………5分
………………………5分
(2)设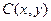 ,
,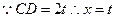 ,代入抛物线方程得
,代入抛物线方程得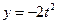 ,故梯形的高为
,故梯形的高为
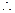
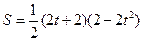 =
=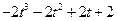 …………………9分
…………………9分
又由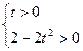 解得
解得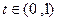
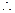 其定义域为
其定义域为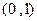 ………………………10分
………………………10分
(3)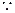
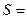
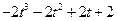 ,
, 
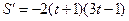
令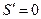 ,解得
,解得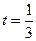 -------------------12分
-------------------12分
当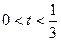 时
时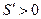
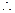 函数在该区间递增,
函数在该区间递增,
当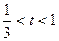 时
时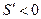
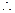 函数在该区间递减, ………………………14分
函数在该区间递减, ………………………14分
所以当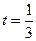 时函数取得最大值,
时函数取得最大值,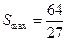 ………………………16分
………………………16分
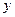 轴建立坐标系,
轴建立坐标系,设抛物线方程为:
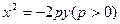 ,
,由图得抛物线过点
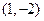 ,代入
,代入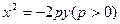 求得
求得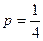 ,
,所以外轮廓线所在抛物线的方程:
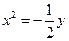 ………………………5分
………………………5分(2)设
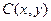 ,
,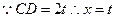 ,代入抛物线方程得
,代入抛物线方程得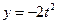 ,故梯形的高为
,故梯形的高为
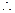
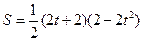 =
=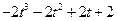 …………………9分
…………………9分又由
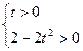 解得
解得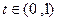
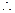 其定义域为
其定义域为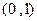 ………………………10分
………………………10分(3)
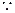
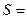
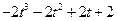 ,
, 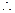
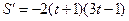
令
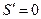 ,解得
,解得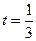 -------------------12分
-------------------12分当
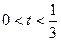 时
时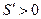
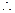 函数在该区间递增,
函数在该区间递增,当
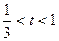 时
时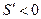
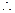 函数在该区间递减, ………………………14分
函数在该区间递减, ………………………14分所以当
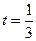 时函数取得最大值,
时函数取得最大值,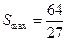 ………………………16分
………………………16分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
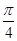 的直线
的直线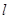 通过抛物线
通过抛物线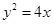 的焦点且与抛物线相交于
的焦点且与抛物线相交于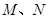 两点,则线段
两点,则线段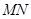 的长为
的长为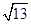
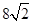
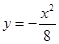 的准线方程是( )
的准线方程是( )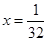
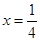
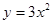 的焦点坐标是
的焦点坐标是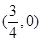
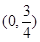
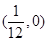
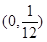
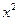 =4y的焦点为F,经过点P(1,4)的直线l与抛物线相交于A、B两点,且点P恰为AB的中点,则|
=4y的焦点为F,经过点P(1,4)的直线l与抛物线相交于A、B两点,且点P恰为AB的中点,则|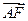 |+|
|+|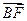 |=________________.
|=________________.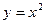 上不存在关于直线
上不存在关于直线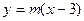 对称的两点,则
对称的两点,则 的取值范围是
的取值范围是 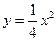 上的动点
上的动点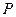 到直线
到直线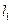 :
: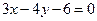 和直线
和直线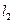 :
: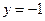 的距离之和得最小值是
的距离之和得最小值是 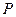 到点
到点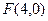 的距离比它到直线
的距离比它到直线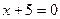 的距离少1,则动点
的距离少1,则动点 的顶点,过点D(0,4)的直线
的顶点,过点D(0,4)的直线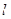 交抛物线
交抛物线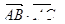 等于( )
等于( )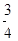 B.0 C.-3 D.
B.0 C.-3 D.