Question

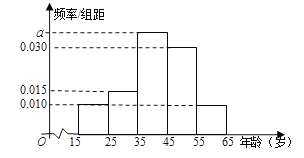
【题目】十九大提出，坚决打赢脱贫攻坚战，某帮扶单位为帮助定点扶贫村真脱贫，坚持扶贫同扶智相结合，帮助贫困村种植蜜柚，并利用电商进行销售，为了更好地销售，现从该村的蜜柚树上随机摘下了100个蜜柚进行测重，其质量分别在，，，，，（单位：克）中，其频率分布直方图如图所示.

（1）按分层抽样的方法从质量落在，的蜜柚中抽取5个，再从这5个蜜柚中随机抽取2个，求这2个蜜柚质量均小于2000克的概率；

（2）以各组数据的中间数代表这组数据的平均水平，以频率代表概率，已知该贫困村的蜜柚树上大约还有5000个蜜柚等待出售，某电商提出两种收购方案：

A. 所有蜜柚均以40元/千克收购；

B. 低于2250克的蜜柚以60元/个收购，高于或等于2250克的以80元/个收购.

请你通过计算为该村选择收益最好的方案.

Answer 1

【答案】（1） （2）选择方案，理由见解析

【解析】

(1)由题得蜜柚质量在和的比例为2：3,应分别在质量为,的蜜柚中各抽取2个和3个.记抽取质量在的蜜柚为,,质量在的蜜柚为,,,则从这5个蜜柚中随机抽取2个,利用列举法能求出这2个蜜柚质量均小于2000克的概率.

(2)由频率分布直方图可知,蜜柚质量在的频率为0.1,蜜柚质量在,,,的频率依次为0.1,0.15,0.4,0.2,0.05.

若按方案收购：根据题意各段蜜柚个数依次为500,500,750,2000,1000,250,求出总收益为457500（元）；

若按方案收购：收益为元.

方案的收益比方案的收益高,应该选择方案.

解：（1）由题得蜜柚质量在和的比例为,

∴应分别在质量为,的蜜柚中各抽取2个和3个.

记抽取质量在的蜜柚为,,质量在的蜜柚为,,,

则从这5个蜜柚中随机抽取2个的情况共有以下10种：

,,,,,,,,,,

其中质量均小于2000克的仅有这1种情况,

故这2个蜜柚质量均小于2000克的概率为.

（2）方案好,理由如下：

由频率分布直方图可知,蜜柚质量在的频率为,

同理,蜜柚质量在,,

,的频率依次为0.1,0.15,0.4,0.2,0.05.

若按方案收购：

根据题意各段蜜柚个数依次为500,500,750,2000,1000,250,

于是总收益为

（元）

若按方案收购：

∵蜜柚质量低于2250克的个数为,

蜜柚质量低于2250克的个数为,

∴收益为元.

∴方案的收益比方案的收益高,应该选择方案.