题目内容
【题目】设点![]() 是
是![]() 所在平面内一点,下列说法正确的是( )
所在平面内一点,下列说法正确的是( )
A.若![]() ,则
,则![]() 的形状为等边三角形
的形状为等边三角形
B.若![]() ,则点
,则点![]() 是边
是边![]() 的中点
的中点
C.过![]() 任作一条直线,再分别过顶点
任作一条直线,再分别过顶点![]() 作
作![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,若
,若![]() 恒成立,则点
恒成立,则点![]() 是
是![]() 的垂心
的垂心
D.若![]() 则点
则点![]() 在边
在边![]() 的延长线上
的延长线上
【答案】AB
【解析】
对于A,由![]() ,利用投影通过三线合一判断
,利用投影通过三线合一判断![]() ;对于B:由
;对于B:由![]() ,变形为
,变形为![]() 判断;对于C:将此直线特殊为过点
判断;对于C:将此直线特殊为过点![]() ,则
,则![]() ,有
,有![]() ,则直线
,则直线![]() 经过
经过![]() 的中点判断;对于D:由
的中点判断;对于D:由![]() ,变形为
,变形为![]() 判断.
判断.
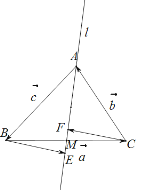
对于A选项,如图所示.

作![]() 于
于![]() ,则
,则![]() ,
,
因为![]() ,
,
所以![]() 为
为![]() 的中点,
的中点,
![]() .同理可证
.同理可证![]() ,
,
![]() 为等边三角形.故A正确.
为等边三角形.故A正确.
对于B选项:![]() ,
,
即:![]() ,则点
,则点![]() 是边
是边![]() 的中点,故B正确;
的中点,故B正确;
对于C选项:因为过![]() 内一点
内一点![]() 任作一条直线,可将此直线特殊为过点
任作一条直线,可将此直线特殊为过点![]() ,
,
则![]() ,有
,有![]() .
.
如图:
则有直线![]() 经过
经过![]() 的中点,
的中点,
同理可得直线![]() 经过
经过![]() 的中点,直线
的中点,直线![]() 经过
经过![]() 的中点,
的中点,
所以点![]() 是
是![]() 的重心,故C错误.
的重心,故C错误.
对于D选项:![]() ,
,![]() ,
,
则点![]() 在边
在边![]() 的延长线上,故D错误.
的延长线上,故D错误.
故选:AB

练习册系列答案
相关题目
【题目】为了研究黏虫孵化的平均温度![]() (单位:
(单位: ![]() )与孵化天数
)与孵化天数![]() 之间的关系,某课外兴趣小组通过试验得到如下6组数据:
之间的关系,某课外兴趣小组通过试验得到如下6组数据:
组号 | 1 | 2 | 3 | 4 | 5 | 6 |
平均温度 | 15.3 | 16.8 | 17.4 | 18 | 19.5 | 21 |
孵化天数 | 16.7 | 14.8 | 13.9 | 13.5 | 8.4 | 6.2 |
他们分别用两种模型①![]() ,②
,②![]() 分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图:
分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图:

经计算得![]() ,
,
(1)根据残差图,比较模型①,②的拟合效果,应选择哪个模型?(给出判断即可,不必说明理由)
(2)残差绝对值大于1的数据被认为是异常数据,需要剔除,剔除后应用最小二乘法建立![]() 关于
关于![]() 的线性回归方程.(精确到0.1)
的线性回归方程.(精确到0.1)
 ,.
,.

