题目内容
【题目】过椭圆![]() 的右焦点F作直线
的右焦点F作直线![]() 交椭圆于M、N两点,H为线段MN的中点,且OH的斜率为
交椭圆于M、N两点,H为线段MN的中点,且OH的斜率为![]() ,设点
,设点![]()
![]() 求该椭圆的方程;
求该椭圆的方程;
![]() 若点P是椭圆上的动点,求线段PA的中点G的轨迹方程;
若点P是椭圆上的动点,求线段PA的中点G的轨迹方程;
![]() 过原点的直线交椭圆于B、C两点,求
过原点的直线交椭圆于B、C两点,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)
;(2) ,(3)最大值
,(3)最大值![]() .
.
【解析】
![]() 结合点差法和直线的斜率,以及OH的斜率为
结合点差法和直线的斜率,以及OH的斜率为![]() ,可得
,可得![]() ,再根据右焦点F在直线
,再根据右焦点F在直线![]() 上,求出c,即可求出椭圆的方程;
上,求出c,即可求出椭圆的方程;
![]() 利用转移法解得G的轨迹方程;
利用转移法解得G的轨迹方程;
![]() 联立直线的方程与椭圆方程,利用弦长公式求出CB,再根据点到直线距离公式得A到CB的距离,根据三角形的面积得函数解析式,根据基本不等式求出最大值.
联立直线的方程与椭圆方程,利用弦长公式求出CB,再根据点到直线距离公式得A到CB的距离,根据三角形的面积得函数解析式,根据基本不等式求出最大值.
解:![]() 设
设![]() ,
,![]() 则
则 ,两式相减可得,
,两式相减可得,
![]() ,
,
即![]() ,
,
![]()
![]() 直线
直线![]() 交椭圆于M、N两点,H为线段MN的中点,且OH的斜率为
交椭圆于M、N两点,H为线段MN的中点,且OH的斜率为![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]()
![]() 右焦点F作在直线
右焦点F作在直线![]() 上,
上,
令![]() ,可得
,可得![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
由![]() ,解得
,解得![]() ,
,![]() ,
,
![]() 椭圆方程为
椭圆方程为![]() ;
;
![]() 设
设![]() ,
,![]() ,则有
,则有 ,即
,即 ,代入为
,代入为![]() 中,
中,
得![]() ,
,
故线段PA的中点G的轨迹方程为 ,
,
![]() 当直线BC垂直x轴时,此时
当直线BC垂直x轴时,此时![]() ,点A到直线BC的距离
,点A到直线BC的距离![]() ,则
,则![]() ,
,
当直线BC的斜率为零时,此时![]() ,点A到直线BC的距离
,点A到直线BC的距离![]() ,则
,则![]() ,
,
当直线BC的斜率存在且不为零时,设直线BC的方程为![]() ,
,
联立方程组可得 ,消y整理可得
,消y整理可得![]() ,
,
解得![]() ,
,![]() ,
,
则![]() ,
,
点A到直线BC的距离![]() ,
,
![]()
![]() ,
,
![]() ,
,
当且仅当![]() 时,即
时,即![]() ,
,![]() 取最大值,最大值为
取最大值,最大值为![]() ,
,
综上所述![]() 面积的最大值
面积的最大值![]() .
.

【题目】小明在石家庄市某物流派送公司找到了一份派送员的工作,该公司给出了两种日薪薪酬方案.甲方案:底薪100元,每派送一单奖励1元;乙方案:底薪140元,每日前55单没有奖励,超过55单的部分每单奖励12元.
(1)请分别求出甲、乙两种薪酬方案中日薪![]() (单位:元)与送货单数
(单位:元)与送货单数![]() 的函数关系式;
的函数关系式;
(2)根据该公司所有派送员100天的派送记录,发现派送员的日平均派送单数与天数满足以下表格:
日均派送单数 | 52 | 54 | 56 | 58 | 60 |
频数(天) | 20 | 30 | 20 | 20 | 10 |
回答下列问题:
①根据以上数据,设每名派送员的日薪为![]() (单位:元),试分别求出这100天中甲、乙两种方案的日薪
(单位:元),试分别求出这100天中甲、乙两种方案的日薪![]() 平均数及方差;
平均数及方差;
②结合①中的数据,根据统计学的思想,帮助小明分析,他选择哪种薪酬方案比较合适,并说明你的理由.
(参考数据: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() )
)
【答案】(1) ;(2)见解析
;(2)见解析
【解析】试题分析:(1)甲方案:底薪100元,每派送一单奖励1元;乙方案:底薪140元,每日前55单没有奖励,超过55单的部分每单奖励12元. 求出甲、乙两种薪酬方案中日薪![]() (单位:元)与送货单数
(单位:元)与送货单数![]() 的函数关系式;
的函数关系式;
①、由表格可知,甲方案中,日薪为152元的有20天,日薪为154元的有30天,日薪为156元的有20天,日薪为158元的有20天,日薪为160元的有10天,由此可求出这100天中甲方案的日薪![]() 平均数及方差:同理可求出这100天中乙两种方案的日薪
平均数及方差:同理可求出这100天中乙两种方案的日薪![]() 平均数及方差,
平均数及方差,
②不同的角度可以有不同的答案
试题解析:((1)甲方案中派送员日薪![]() (单位:元)与送货单数
(单位:元)与送货单数![]() 的函数关系式为:
的函数关系式为: ![]() ,
,
乙方案中派送员日薪![]() (单位:元)与送单数
(单位:元)与送单数![]() 的函数关系式为:
的函数关系式为:
![]() ,
,
(2)①、由表格可知,甲方案中,日薪为152元的有20天,日薪为154元的有30天,日薪为156元的有20天,日薪为158元的有20天,日薪为160元的有10天,则
![]()
![]() ,
,
 ,
,
乙方案中,日薪为140元的有50天,日薪为152元的有20天,日薪为176元的有20天,日薪为200元的有10天,则
![]()
![]() ,
,
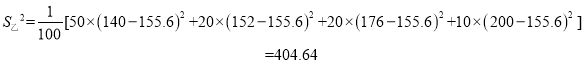
②、答案一:
由以上的计算可知,虽然![]() ,但两者相差不大,且
,但两者相差不大,且![]() 远小于
远小于![]() ,即甲方案日薪收入波动相对较小,所以小明应选择甲方案.
,即甲方案日薪收入波动相对较小,所以小明应选择甲方案.
答案二:
由以上的计算结果可以看出, ![]() ,即甲方案日薪平均数小于乙方案日薪平均数,所以小明应选择乙方案.
,即甲方案日薪平均数小于乙方案日薪平均数,所以小明应选择乙方案.
【题型】解答题
【结束】
20
【题目】已知椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
, ![]() ,且离心率为
,且离心率为![]() ,
, ![]() 为椭圆上任意一点,当
为椭圆上任意一点,当![]() 时,
时, ![]() 的面积为1.
的面积为1.
(1)求椭圆![]() 的方程;
的方程;
(2)已知点![]() 是椭圆
是椭圆![]() 上异于椭圆顶点的一点,延长直线
上异于椭圆顶点的一点,延长直线![]() ,
, ![]() 分别与椭圆交于点
分别与椭圆交于点![]() ,
, ![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求证:
,求证: ![]() 为定值.
为定值.
【题目】汕尾市基础教育处为调查在校中学生每天放学后的自学时间情况,在本市的所有中学生中随机抽取了120名学生进行调查,现将日均自学时间小于1小时的学生称为“自学不足”者![]() 根据调查结果统计后,得到如下
根据调查结果统计后,得到如下![]() 列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为
列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为![]() .
.
非自学不足 | 自学不足 | 合计 | |
配有智能手机 | 30 | ||
没有智能手机 | 10 | ||
合计 |
![]() 请完成上面的列联表;
请完成上面的列联表;
![]() 根据列联表的数据,能否有
根据列联表的数据,能否有![]() 的把握认为“自学不足”与“配有智能手机”有关?
的把握认为“自学不足”与“配有智能手机”有关?
附表及公式: ![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|








