题目内容
在 中,满足
中,满足 ,
, .若一个椭圆恰好以
.若一个椭圆恰好以 为一个焦点,另一个焦点在线段
为一个焦点,另一个焦点在线段 上,且
上,且 ,
, 均在此椭圆上,则该椭圆的离心率为 .
均在此椭圆上,则该椭圆的离心率为 .
 中,满足
中,满足 ,
, .若一个椭圆恰好以
.若一个椭圆恰好以 为一个焦点,另一个焦点在线段
为一个焦点,另一个焦点在线段 上,且
上,且 ,
, 均在此椭圆上,则该椭圆的离心率为 .
均在此椭圆上,则该椭圆的离心率为 .
解:因为根据已知直角三角形可知斜边长为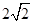 ,然后利用椭圆的定义得到长半轴的长和焦距的值,从而得到离心率为
,然后利用椭圆的定义得到长半轴的长和焦距的值,从而得到离心率为
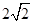 ,然后利用椭圆的定义得到长半轴的长和焦距的值,从而得到离心率为
,然后利用椭圆的定义得到长半轴的长和焦距的值,从而得到离心率为

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目

 的离心率为
的离心率为 =
= ,点
,点 是椭圆上的一点,且点
是椭圆上的一点,且点 两焦点的距离之和为4.
两焦点的距离之和为4.
 关于直线
关于直线 的对称点为
的对称点为 ,求
,求 的取值范围.
的取值范围. 是把坐标平面上的点的横坐标伸长为原来的4倍,纵坐标伸长为原来的3倍的伸压变换,则圆
是把坐标平面上的点的横坐标伸长为原来的4倍,纵坐标伸长为原来的3倍的伸压变换,则圆 在
在 上一点
上一点 到右准线的距离为
到右准线的距离为 ,则该点到左焦点的距离为( )
,则该点到左焦点的距离为( ) 



 与椭圆
与椭圆 相交于A、B两点.
相交于A、B两点. ,焦距为2,求线段AB的长;
,焦距为2,求线段AB的长; 与向量
与向量 互相垂直(其中O为坐标原点),当椭圆的离心率
互相垂直(其中O为坐标原点),当椭圆的离心率 时,求椭圆的长轴长的最大值.
时,求椭圆的长轴长的最大值. 的左、右焦点分别为
的左、右焦点分别为 ,若以
,若以 为圆心,
为圆心, 为半径作圆
为半径作圆 作此圆的切线,切点为
作此圆的切线,切点为 ,且
,且 的最小值不小于为
的最小值不小于为 .
. 的取值范围;
的取值范围; ,圆
,圆 轴的右交点为
轴的右交点为 ,过点
,过点 的直线
的直线 与椭圆相交于
与椭圆相交于 两点,若
两点,若 ,求直线
,求直线 的最大值.
的最大值.
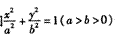 长轴上有一点到两个焦点之间的距离分别为:3+2
长轴上有一点到两个焦点之间的距离分别为:3+2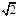 ,3-2
,3-2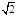
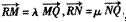 ,求证:
,求证: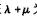 为定值.
为定值.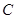 :
: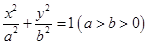 的离心率为
的离心率为 ,
,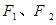 分别为椭圆
分别为椭圆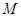 为椭圆上任意一点,以
为椭圆上任意一点,以 为半径作圆
为半径作圆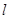 有公共点时,求△
有公共点时,求△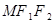 面积的最大值.
面积的最大值. 与双曲线
与双曲线 有相同的焦点, 则m的值为( )
有相同的焦点, 则m的值为( )


