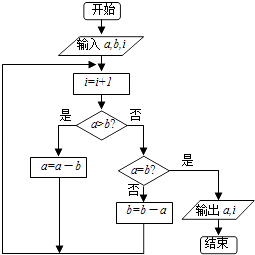
题目内容
【题目】为了体现国家“民生工程”,某市政府为保障居民住房,现提供一批经济适用房.现有条件相同的甲、已、丙、丁四套住房供A、B、C三人自主申请,他们的申请是相互独立的.
(1)求A、B两人都申请甲套住房的概率;
(2)求A、B两人不申请同一套住房的概率;
(3)设3名参加选房的人员中选择甲套住房的人数为ξ,求ξ的分布列和数学期望.
【答案】
(1)解:设“A申请甲套住房”为事件M1,“B申请甲套住房”为事件M2
那么A,B两人都申请甲套住房的概率
![]()
所以甲、乙两人都申请甲套住房的概率为 ![]()
(2)解:设“A,B两人选择同一套住房”为事件N,
![]()
所以A,B两人不选择同一套住房的概率是
![]()
(3)解:(方法一)随机变量ξ可能取的值为0,1,2,3,那么 ![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
所以ξ的分布列为
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
所以 ![]()
(方法二)依题意得 ![]()
所以ξ的分布列为 ![]() ,k=0,1,2,3.
,k=0,1,2,3.
即
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
所以 ![]()
【解析】(1)设“A申请甲套住房”为事件M1 , “B申请甲套住房”为事件M2 . 由事件A和B是独立事件,能求出A,B两人都申请甲套住房的概率.(2)设“A,B两人选择同一套住房”为事件N,先求出事件N的概率,再求A,B两人不选择同一套住房的概率.(3)法一:随机变量ξ可能取的值为0,1,2,3,分别求出P(ξ=0),P(ξ=1),P(ξ=2),P(ξ=3),由此能求出ξ的分布列和Eξ.法二:依题意得 ![]() ,由此能求出ξ的分布列和Eξ.
,由此能求出ξ的分布列和Eξ.

【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问部分职工,根据被访问职工对该部门的评分,绘制频率分布直方图(如图所示).
(1)求频率分布表中①、②、③位置相应数据,并在答题纸上完成频率分布直方图;
组号 | 分组 | 频数 | 频率 |
第1组 | [50,60) | 5 | 0.050 |
第2组 | [60,70) | ① | 0.350 |
第3组 | [70,80) | 30 | ② |
第4组 | [80,90) | 20 | 0.200 |
第5组 | [90,100] | 10 | 0.100 |
合计 | ③ | 1.00 | |
(2)为进一步了解情况,该企业决定在第3,4,5组中用分层抽样抽取5名职工进行座谈,求第3,4,5组中各自抽取的人数;
(3)求该样本平均数 ![]() .
.