题目内容
【题目】已知函数y=f(x)是定义在R上的增函数,函数y=f(x﹣1)的图象关于(1,0)对称.若对任意的x,y∈R,不等式f(x2﹣6x+21)+f(y2﹣8y)<0恒成立,则当x>3时,x2+y2的取值范围是( )
A.(9,25)
B.(13,49)
C.(3,7)
D.(9,49)
【答案】B
【解析】解:∵函数y=f(x﹣1)的图象关于点(1,0)对称,
∴函数y=f(x)的图象关于点(0,0)对称,
即函数y=f(x)为奇函数,则f(﹣x)=﹣f(x),
又∵f(x)是定义在R上的增函数且f(x2﹣6x+21)+f(y2﹣8y)<0恒成立
∴f(x2﹣6x+21)<﹣f(y2﹣8y)=f(8y﹣y2)恒成立,
∴x2﹣6x+21<8y﹣y2 ,
∴(x﹣3)2+(y﹣4)2<4恒成立,
设M (x,y),则当x>3时,M表示以(3,4)为圆心2为半径的右半圆内的任意一点,
则d= ![]() 表示区域内的点和原点的距离.
表示区域内的点和原点的距离.
由图可知:d的最小值是OA= ![]() ,OB=OC+CB,5+2=7,
,OB=OC+CB,5+2=7,
当x>3时,x2+y2的范围为(13,49).
故选B.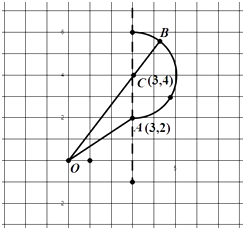

 阅读快车系列答案
阅读快车系列答案【题目】我市2016年11月1日![]() 11月30日对空气污染指数的监测数据如下(主要污染物可吸入颗粒物):61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,83,82,82,64,79,86,85,75,71,49,45.
11月30日对空气污染指数的监测数据如下(主要污染物可吸入颗粒物):61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,83,82,82,64,79,86,85,75,71,49,45.
样本频率分布表:
分组 | 频数 | 频率 |
| 2 |
|
| 1 |
|
| 4 |
|
| 6 |
|
| 10 |
|
| ||
| 2 |
|
(Ⅰ)完成频率分布表;
(Ⅱ)作出频率分布直方图;
(Ⅲ)根据国家标准,污染指数在0![]() 50之间时,空气质量为优;在51
50之间时,空气质量为优;在51![]() 100之间时为良;在101
100之间时为良;在101![]() 150之间时,为轻微污染;在151
150之间时,为轻微污染;在151![]() 200之间时,为轻度污染.请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.
200之间时,为轻度污染.请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.