题目内容
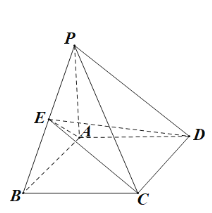
【题目】如图，四棱锥
中，底面
为矩形，
底面，
，
，点
是棱
的中点.直线
与平面
的距离为（ ）
A.
B.
C.
D.
【答案】B
【解析】
根据
底面
，得到
，再由底面为矩形，得到
，利用线面垂直的判定定理得到 
平面
，从而得到平面
平面，则点A到FD的距离，即点A到平面
的距离，根据
，则
平面，则点A到平面的距离，即为直线AB到平面的距离，然后在
中求解.
如图所示：
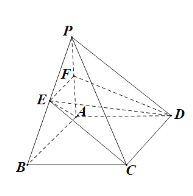
取PA的中点F，连接EF，FD，
因为底面，所以，
因为底面为矩形，所以，
，
所以平面，又
平面，
所以平面平面，平面
平面
，
所以点A到FD的距离，即为点A到平面的距离，
因为，
平面，
平面，
所以平面，
所以点A到平面的距离，即为直线AB到平面的距离，
在中，
，
所以点A到FD的距离为
.
故直线
与平面
的距离为
.
故选：B
【题目】某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四次试验，得到的数据如下：
零件的个数 | 2 | 3 | 4 | 5 |
加工的时间 | 2.5 | 3 | 4 | 4.5 |
（1）在给定的坐标系中画出表中数据的散点图；
（2）求出
关于
的线性回归方程
，并在坐标系中画出回归直线；
（3）试预测加工
个零件需要多少时间？
参考公式：回归直线，其中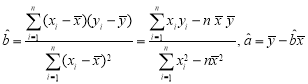
.
【题目】某产品的三个质量指标分别为x, y, z, 用综合指标S =" x" + y + z评价该产品的等级. 若S≤4, 则该产品为一等品. 现从一批该产品中, 随机抽取10件产品作为样本, 其质量指标列表如下:
产品编号 | A1 | A2 | A3 | A4 | A5 |
质量指标(x, y, z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
产品编号 | A6 | A7 | A8 | A9 | A10 |
质量指标(x, y, z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(Ⅰ) 利用上表提供的样本数据估计该批产品的一等品率;
(Ⅱ) 在该样品的一等品中, 随机抽取两件产品,
(1) 用产品编号列出所有可能的结果;
(2) 设事件B为 “在取出的2件产品中, 每件产品的综合指标S都等于4”, 求事件B发生的概率.
