题目内容
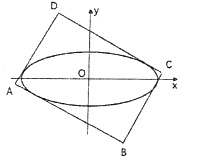
【题目】已知抛物线![]() ,
,![]() 为其焦点,椭圆
为其焦点,椭圆![]() ,
,![]() ,
,![]() 为其左右焦点,离心率
为其左右焦点,离心率![]() ,过
,过![]() 作
作![]() 轴的平行线交椭圆于
轴的平行线交椭圆于![]() 两点,
两点,![]() .
.
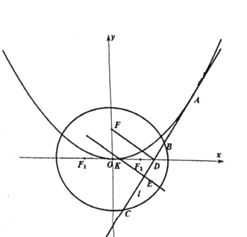
(1)求椭圆的标准方程;
(2)过抛物线上一点![]() 作切线
作切线![]() 交椭圆于
交椭圆于![]() 两点,设
两点,设![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
,![]() 的中点为
的中点为![]() ,
,![]() 的中垂线交
的中垂线交![]() 轴为
轴为![]() ,
,![]() ,
,![]() 的面积分别记为
的面积分别记为![]() ,
,![]() ,若
,若![]() ,且点
,且点![]() 在第一象限.求点
在第一象限.求点![]() 的坐标.
的坐标.
【答案】(1) ![]() . (2)
. (2) ![]()
【解析】
(1)由题设可知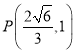 ,又
,又![]() ,把
,把![]() 均用
均用![]() 表示,并把点
表示,并把点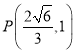 代入标圆方程,求得
代入标圆方程,求得![]() ;
;
(2)根据导数的几可意义求得直线![]() 的方程,根据韦达定理及中点坐标公式求得点
的方程,根据韦达定理及中点坐标公式求得点![]() 的坐标,求得中垂线方程,即可求得
的坐标,求得中垂线方程,即可求得![]() 点坐标,根据三角形面积公式,即可求得点
点坐标,根据三角形面积公式,即可求得点![]() 坐标.
坐标.
(1)不妨设![]() 在第一象限,
在第一象限,
由题可知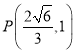 ,
,![]() ,
,
又![]() ,
,![]() ,
,
可得![]() ,椭圆的方程为
,椭圆的方程为![]() .
.

(2)设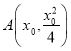 则切线
则切线![]() 的方程为
的方程为![]()
代入椭圆方程得:![]() ,
,
设![]() ,
,
则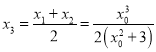 ,
,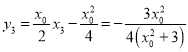 ,
,
![]() 的方程为
的方程为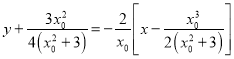 ,
,
即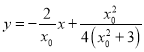 ,
,
令![]() 得
得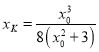 ,
,
在直线![]() 方程中令
方程中令![]() 得
得![]() ,
,
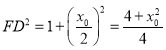
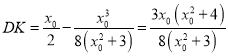 ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,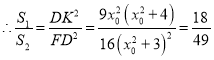 .
.
化简得![]() ,
,
![]() (
(![]() 舍去)
舍去)![]() 的坐标为
的坐标为![]() .
.
![]() ,
,
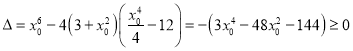 ,
,
因为![]() ,故此解符合题意.
,故此解符合题意.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
【题目】某校共有学生2000人,其中男生1100人,女生900人为了调查该校学生每周平均课外阅读时间,采用分层抽样的方法收集该校100名学生每周平均课外阅读时间(单位:小时)
(1)应抽查男生与女生各多少人?
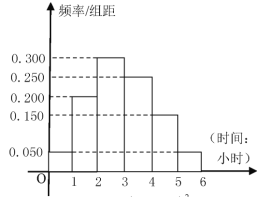
(2)如图,根据收集100人的样本数据,得到学生每周平均课外阅读时间的频率分布直方图,其中样本数据分组区间为![]() .若在样本数据中有38名女学生平均每周课外阅读时间超过2小时,请完成每周平均课外阅读时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均课外阅读时间与性别有关”.
.若在样本数据中有38名女学生平均每周课外阅读时间超过2小时,请完成每周平均课外阅读时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均课外阅读时间与性别有关”.
男生 | 女生 | 总计 | |
每周平均课外阅读时间不超过2小时 | |||
每周平均课外阅读时间超过2小时 | |||
总计 |
附:
| 0.100 | 0.050 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |