题目内容
极坐标方程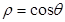 和参数方程
和参数方程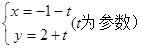 所表示的图形分别是( )
所表示的图形分别是( )
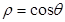 和参数方程
和参数方程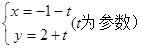 所表示的图形分别是( )
所表示的图形分别是( )| A.直线,直线 | B.直线,圆 |
| C.圆,圆 | D.圆,直线 |
D
试题分析:
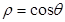 即
即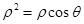 ,所以,
,所以,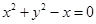 表示圆;
表示圆;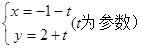 即
即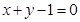 ,表示直线,故选D。
,表示直线,故选D。点评:简单题,注意一般的“消参”方法,涉及正弦、余弦函数,一般采用平方关系消元法。极坐标中应用:
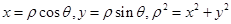 等。
等。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
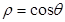 和参数方程
和参数方程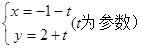 所表示的图形分别是( )
所表示的图形分别是( )| A.直线,直线 | B.直线,圆 |
| C.圆,圆 | D.圆,直线 |
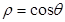 即
即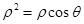 ,所以,
,所以,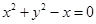 表示圆;
表示圆;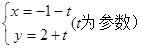 即
即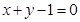 ,表示直线,故选D。
,表示直线,故选D。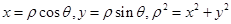 等。
等。
 阅读快车系列答案
阅读快车系列答案