题目内容
双曲线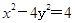 的离心率为
的离心率为
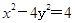 的离心率为
的离心率为A.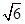 | B.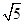 | C.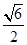 | D.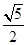 |
D
试题分析:根据题意,由于双曲线
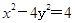 化为标准式为
化为标准式为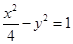 ,焦点在x轴上,同时a=2,b=1,c=
,焦点在x轴上,同时a=2,b=1,c=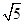 那么根据离心率e=c:a=
那么根据离心率e=c:a=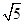 :2,故可知答案为D。
:2,故可知答案为D。点评:本题主要考查双曲线的几何性质,求双曲线的离心率,应注意焦点的位置,避免错解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
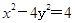 的离心率为
的离心率为A.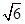 | B.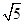 | C.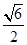 | D.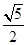 |
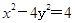 化为标准式为
化为标准式为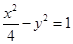 ,焦点在x轴上,同时a=2,b=1,c=
,焦点在x轴上,同时a=2,b=1,c=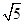 那么根据离心率e=c:a=
那么根据离心率e=c:a=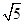 :2,故可知答案为D。
:2,故可知答案为D。
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案