题目内容
7.(1)一直线过点(1,2),并且与点(2,3)和(0,-5)的距离相等,求此直线的方程.(2)已知等比数列{an}中,a3=1$\frac{1}{2}$,前3项和S3=4$\frac{1}{2}$,求a1和公比q.
分析 (1)根据题意和斜率公式求出直线的斜率,代入点斜式方程再化为一般式方程即可;
(2)由等比数列的通项公式和前n项和定义列出方程组,求出a1和公比q.
解答 解:(1)∵一直线过点(1,2),且与点(2,3)和(0,-5)的距离相等,
∴直线斜率k=$\frac{-5-3}{0-2}$=4,
∴直线方程是y-2=4(x-1),即4x-y-2=0;
(2)∵等比数列{an}中,a3=1$\frac{1}{2}$.前3项和S3=4$\frac{1}{2}$,
∴$\left\{\begin{array}{l}{{a}_{1}{q}^{2}=\frac{3}{2}}\\{{a}_{1}+{a}_{1}q+{a}_{1}{q}^{2}=\frac{9}{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}_{1}=6}\\{q=-\frac{1}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{{a}_{1}=\frac{3}{2}}\\{q=1}\end{array}\right.$,
∴a1=6、q=$-\frac{1}{2}$或a1=$\frac{3}{2}$、q=1.
点评 本题考查等比数列的通项公式和前n项和定义,以及直线点斜式、一般式方程的应用,属于基础题.

练习册系列答案
相关题目
15.在△ABC中,若c2+ab=a2+b2,则角C=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
2.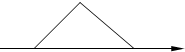 用斜二测画法得到某三角形的水平放置的直观图是一个等腰直角三角形(如图所示,其中的x轴表示水平方向),斜边长为2,则原三角形的面积为( )
用斜二测画法得到某三角形的水平放置的直观图是一个等腰直角三角形(如图所示,其中的x轴表示水平方向),斜边长为2,则原三角形的面积为( )
 用斜二测画法得到某三角形的水平放置的直观图是一个等腰直角三角形(如图所示,其中的x轴表示水平方向),斜边长为2,则原三角形的面积为( )
用斜二测画法得到某三角形的水平放置的直观图是一个等腰直角三角形(如图所示,其中的x轴表示水平方向),斜边长为2,则原三角形的面积为( )| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | 4 |
12.执行如图的程序框图,若输入m的值为2,则输出的结果i=( )
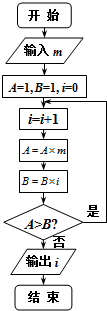

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
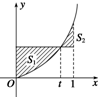 在区间[0,1]上给定曲线y=x2,如图所示,0<t<1,S1,S2是t的函数,则函数g(t)=S1+S2的单调递增区间为($\frac{1}{2}$,1).
在区间[0,1]上给定曲线y=x2,如图所示,0<t<1,S1,S2是t的函数,则函数g(t)=S1+S2的单调递增区间为($\frac{1}{2}$,1).