题目内容
19．
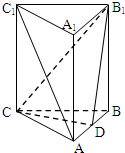如图所示，在所有棱长都为2a的三棱柱ABC-A1B1C1中，侧棱AA1⊥平面ABC，D点为棱AB的中点．（1）求证：AC1∥平面CDB1；
（2）求四棱锥C1-ADB1A1的体积．
分析 （1）要证AC1∥平面CDB1，可采用线面平行的判定定理，故可连结BC1，得到BC1与B1C交点E，则DE是△ABC1的中位线，由此证得答案；
（2）取线段A1B1中点M，连结C1M，由已知可证得C1M是四棱锥C1-ADB1A1的高，再由已知求出平面
ADB1A1的面积，代入棱锥的体积公式得答案．
解答 （1）证明：如图，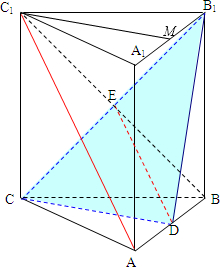
连结BC1，设BC1与B1C交于点E，
则点E是BC1的中点，连结DE，
∵D点为AB的中点，
∴DE是△ABC1的中位线，
∴AC1∥DE，
∵DE?平面CDB1，AC1?面CDB1，
∴AC1∥平面CDB1；
（2）取线段A1B1中点M，连结C1M，
∵C1A1=C1B1，点M为线段A1B1中点，
∴C1M⊥A1B1．
又A1A⊥平面ABC，
即A1A⊥平面C1A1B1，C1M?平面C1A1B1，
∴A1A⊥C1M，
∵A1A∩A1B1=A1，
∴C1M⊥平面ADB1A1，则C1M是四棱锥C1-ADB1A1的高．
则${V}_{{C}_{1}-AD{B}_{1}{A}_{1}}$=$\frac{1}{3}×\frac{（2a+a）×2a}{2}×\sqrt{3}a=\sqrt{3}{a}^{3}$．
点评 本小题主要考查空间线面关系、几何体的体积等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力，是中档题．
练习册系列答案
相关题目
10．已知等边△ABC，边长为1，则|3$\overrightarrow{AB}$+4$\overrightarrow{BC}$|等于（ ）
| A． | $\sqrt{37}$ | B． | 5 | C． | $\sqrt{13}$ | D． | 7 |
14．已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1，过其左焦点F作圆x2+y2=a2的两条切线，切点记作C，D，原点为O，∠COD=$\frac{2π}{3}$，其双曲线的离心率为（ ）
| A． | $\frac{3}{2}$ | B． | 2 | C． | $\sqrt{3}$ | D． | $\frac{{2\sqrt{3}}}{3}$ |
4．若复数z1=$\frac{6+2i}{1-i}$与z2=a+bi（a，b∈R）互为共轭复数，则（ ）
| A． | a=2，b=-4 | B． | a=2，b=4 | C． | a=-2，b=-4 | D． | a=-2，b=4 |
8．
执行如图所示的程序框图，则输出的n的值为（ ）
执行如图所示的程序框图，则输出的n的值为（ ）| A． | 7 | B． | 15 | C． | 31 | D． | 63 |