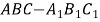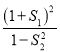题目内容
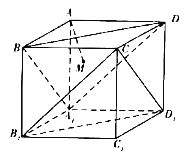
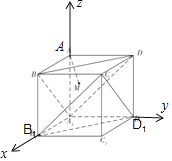
【题目】如图,在正方体ABCD﹣A1B1C1D1中,AM⊥平面A1BD,垂足为M,以下四个结论中正确的个数为( )
①AM垂直于平面CB1D1;
②直线AM与BB1所成的角为45°;
③AM的延长线过点C1;
④直线AM与平面A1B1C1D1所成的角为60°
A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】
①根据AM⊥平面A1BD,平面A1BD∥CB1D1,判断AM⊥平面CB1D1;
②建立空间直角坐标系,利用坐标表示向量,求出平面BDA1的法向量![]() ,求得
,求得![]() 与
与![]() 的夹角,判断直线AM与BB1所成的角不是45°;
的夹角,判断直线AM与BB1所成的角不是45°;
③求出![]() ,判断它与平面CB1D1的法向量
,判断它与平面CB1D1的法向量![]() 共线,得出AM的延长线过点C1;
共线,得出AM的延长线过点C1;
④求出AC1与平面A1B1C1D1所成的角,即为直线AM与平面A1B1C1D1所成的角.
对于①,正方体ABCD﹣A1B1C1D1中,AM⊥平面A1BD,
且平面A1BD∥CB1D1,∴AM⊥平面CB1D1,①正确;
对于②,建立空间直角坐标系,如图所示,
则A(0,0,1),B(1,0,1),C(1,1,1),D(0,1,1),
A1(0,0,0),∴![]() =(﹣1,1,0),
=(﹣1,1,0),![]() =(1,0,1),
=(1,0,1),
设平面BDA1的法向量为![]() =(x,y,z),
=(x,y,z),
则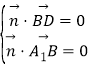 ,即
,即![]() ,令x=1,则y=1,z=﹣1,∴
,令x=1,则y=1,z=﹣1,∴![]() =(1,1,﹣1),
=(1,1,﹣1),
![]() =(0,0,1),
=(0,0,1),
∴cos<![]() ,
,![]() >=
>=![]() =﹣
=﹣![]() ,
,
∴![]() 与
与![]() 的夹角不是45°且不是135°,
的夹角不是45°且不是135°,
又![]() 与
与![]() 共线,∴直线AM与BB1所成的角不是45°,②错误;
共线,∴直线AM与BB1所成的角不是45°,②错误;
对于③,![]() =(1,1,﹣1),与平面CB1D1的法向量
=(1,1,﹣1),与平面CB1D1的法向量![]() 共线,
共线,
∴![]() 与
与![]() 共线,即AM的延长线过点C1,③正确;
共线,即AM的延长线过点C1,③正确;
④![]() 与
与![]() 共线,且tan∠AC1A1=
共线,且tan∠AC1A1=![]() =
=![]() ,
,
∴AC1与平面A1B1C1D1所成的角是arctan![]() ,
,
即直线AM与平面A1B1C1D1所成的角不是60°,④错误;
综上,正确的命题序号是①③,共2个.
故选:B.

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案【题目】一只药用昆虫的产卵数y与一定范围内的温度x有关,现收集了该种药用昆虫的6组观测数据如下表:
温度x/℃ | 21 | 23 | 24 | 27 | 29 | 32 |
产卵数y/个 | 6 | 11 | 20 | 27 | 57 | 77 |
经计算得:
![]() ,
,![]() ,
,![]() 线性回归模型的残差平方和
线性回归模型的残差平方和![]() ,
,![]() ,
,
其中![]() 分别为观测数据中的温度和产卵数,
分别为观测数据中的温度和产卵数,![]()
(1)若用线性回归模型,求y关于x的回归方程![]() (精确到0.1);
(精确到0.1);
(2)若用非线性回归模型求得y关于x的回归方程为![]() ,且相关指数
,且相关指数![]() .
.
①试与1中的回归模型相比,用![]() 说明哪种模型的拟合效果更好.
说明哪种模型的拟合效果更好.
②用拟合效果好的模型预测温度为35℃时该用哪种药用昆虫的产卵数(结果取整数)
附:一组数据![]() 其回归直线
其回归直线![]() 的斜率和截距的最小二乘估计为
的斜率和截距的最小二乘估计为 ,
,![]() ;相关指数
;相关指数 .
.