题目内容
【题目】以下四个关于圆锥曲线的命题:
①设A,B是两个定点,k为非零常数,若|PA|-|PB|=k,则P的轨迹是双曲线;
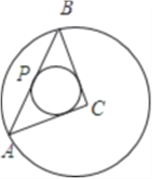
②过定圆C上一定点A作圆的弦AB,O为原点,若![]() .则动点P的轨迹是椭圆;
.则动点P的轨迹是椭圆;
③方程![]() 的两根可以分别作为椭圆和双曲线的离心率;
的两根可以分别作为椭圆和双曲线的离心率;
④双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点.
有相同的焦点.
其中正确命题的序号为________.
【答案】③④
【解析】
①不正确;若动点![]() 的轨迹为双曲线,则
的轨迹为双曲线,则![]() 要小于
要小于![]() 为两个定点间的距离,当点
为两个定点间的距离,当点![]() 在顶点
在顶点![]() 的延长线上时,
的延长线上时,![]() ,显然这种曲线是射线,而非双曲线;②不正确;根据平行四边形法则,易得
,显然这种曲线是射线,而非双曲线;②不正确;根据平行四边形法则,易得![]() 是
是![]() 的中点,根据垂径定理,圆心与弦的中点连线垂直于这条弦,设圆心为
的中点,根据垂径定理,圆心与弦的中点连线垂直于这条弦,设圆心为![]() ,那么有
,那么有![]() 即
即![]() 恒为直角,由于
恒为直角,由于![]() 是圆的半径,是定长,而
是圆的半径,是定长,而![]() 恒为直角,也就是说,
恒为直角,也就是说,![]() 在以
在以![]() 为直径的圆上运动,
为直径的圆上运动,![]() 为直径所对的圆周角,所以
为直径所对的圆周角,所以![]() 点的轨迹是一个圆,如图,③正确;方程
点的轨迹是一个圆,如图,③正确;方程![]() 的两根分别为
的两根分别为![]() 和
和![]() 可分别作为椭圆和双曲线的离心率,④正确,双曲线
可分别作为椭圆和双曲线的离心率,④正确,双曲线![]() 与椭圆
与椭圆![]() 焦点坐标都是
焦点坐标都是![]() ,故答案为③④.
,故答案为③④.

练习册系列答案
相关题目
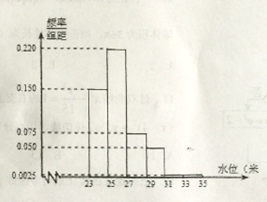
【题目】某学校举行了一次安全教育知识竞赛,竞赛的原始成绩采用百分制,已知高三学生的原始成绩均分布在![]() 内,发布成绩使用等级制,各等级划分标准见表.
内,发布成绩使用等级制,各等级划分标准见表.
原始成绩 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 | 优秀 | 良好 | 及格 | 不及格 |
为了解该校高三年级学生安全教育学习情况,从中抽取了![]() 名学生的原始成绩作为样本进行统计,按照
名学生的原始成绩作为样本进行统计,按照![]() 的分组作出频率分布直方图如图所示,其中等级为不及格的有5人,优秀的有3人.
的分组作出频率分布直方图如图所示,其中等级为不及格的有5人,优秀的有3人.
(1)求![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)根据样本估计总体的思想,以事件发生的频率作为相应事件发生的概率,若该校高三学生共1000人,求竞赛等级在良好及良好以上的人数;
(3)在选取的样本中,从原始成绩在80分以上的学生中随机抽取2名学生进行学习经验介绍,求抽取的2名学生中优秀等级的学生恰好有1人的概率.