题目内容
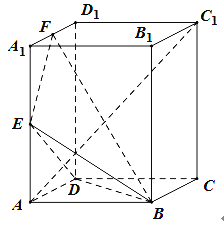
【题目】如图,已知正方形![]() 和矩形
和矩形![]() 所在平面互相垂直,
所在平面互相垂直, ![]() ,
, ![]() .
.

(1)求二面角![]() 的大小;
的大小;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)60°.(2)![]() .
.
【解析】试题分析:(1)先根据条件建立空间直角坐标系,设各点坐标,根据方程组求各面法向量,再根据向量数量积求夹角,最后根据二面角与向量夹角关系得结果(2)根据向量投影得点![]() 到平面
到平面![]() 的距离为
的距离为![]() 再根据向量数量积求值
再根据向量数量积求值
试题解析: ![]() 正方形
正方形![]() 和矩形
和矩形![]() 所在平面互相垂直,
所在平面互相垂直,
分别以AB,AD,AF为x,y,z轴建立空间直角坐标系,
则A(0,0,0),B(![]() ,0,0), C(
,0,0), C(![]() ,
, ![]() ,0), D(0,
,0), D(0, ![]() ,0),
,0),
E(![]() ,
, ![]() ,1),F(0,0,1).
,1),F(0,0,1).
(1)设平面CDE的法向量为![]() 平面BDE的法向量
平面BDE的法向量![]() ,
,
由 解得
解得![]() .
.
∴ ,
,
∴ 二面角 B—DE—C等于60°.
(2)![]()
 ,
,
![]() .设点到平面BDF的距离为h,则
.设点到平面BDF的距离为h,则
∴![]() .所以点F到平面BDE的距离为
.所以点F到平面BDE的距离为![]() .
.

练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
【题目】已知射手甲射击一次,命中9环(含9环)以上的概率为0.56,命中8环的概率为0.22,命中7环的概率为0.12.
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)求甲射击一次,命中不足8环的概率;
(2)求甲射击一次,至少命中7环的概率.