题目内容
【题目】已知A、B、C是△ABC的三个内角,向量m=(-1, ![]() ),n=(cosA,sinA),且m·n=1.
),n=(cosA,sinA),且m·n=1.
(1)求角A;
(2)若![]() =-3,求tanC.
=-3,求tanC.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)由m·n=1,代入坐标用两角和与差的正弦公式化简,即可求出角A;(2)将已知条件用完全平方公式和平方差公式化简,可得![]() =-3,分式上下同除以
=-3,分式上下同除以![]() ,解出
,解出![]() ,又tanC=tan[π-(A+B)],利用诱导公式和两角和与差的正切公式化简,把
,又tanC=tan[π-(A+B)],利用诱导公式和两角和与差的正切公式化简,把![]() 和
和![]() 的值代入即可.
的值代入即可.
试题解析:
(1)∵m·n=1,
∴![]() sinA-cosA=1,2(sinA·
sinA-cosA=1,2(sinA·![]() -cosA·
-cosA·![]() )=1,
)=1,
sin(A-![]() )=
)=![]() ,
,
∵0<A<π,- ![]() <A-
<A-![]() <
<![]() ,
,
∴A-![]() =
=![]() .∴A=
.∴A=![]() .
.
(2)由题知![]() =-3,
=-3,
∴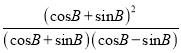 =-3
=-3
∴![]() =-3
=-3
∴![]() =-3,∴tanB=2.
=-3,∴tanB=2.
∴tanC=tan[π-(A+B)]
=-tan(A+B)=-![]() =
=![]() .
.
点睛:本题考查平面向量数量积的坐标运算,同角三角函数的基本关系和两角和与差的正切公式. 平面向量的数量积计算问题,往往有两种形式,一是利用数量积的定义式,二是利用数量积的坐标运算公式,涉及几何图形的问题,先建立适当的平面直角坐标系,可起到化繁为简的妙用. 利用向量夹角公式、模公式及向量垂直的充要条件,可将有关角度问题、线段长问题及垂直问题转化为向量的数量积来解决.列出方程组求解未知数.

【题目】空气质量按照空气质量指数大小分为七档(五级),相对应空气质量的七个类别,指数越大,说明污染的情况越严重,对人体危害越大.
指数 | 级别 | 类别 | 户外活动建议 |
| Ⅰ | 优 | 可正常活动 |
| Ⅱ | 良 | |
| Ⅲ | 轻微污染 | 易感人群症状有轻度加剧,健康人群出现刺激症状,心脏病和呼吸系统疾病患者应减少体积消耗和户外活动. |
| 轻度污染 | ||
| Ⅳ | 中度污染 | 心脏病和肺病患者症状显著加剧,运动耐受力降低,健康人群中普遍出现症状,老年人和心脏病、肺病患者应减少体力活动. |
| 中度重污染 | ||
| Ⅴ | 重污染 | 健康人运动耐受力降低,由明显强烈症状,提前出现某些疾病,老年人和病人应当留在室内,避免体力消耗,一般人群应尽量减少户外活动. |
现统计邵阳市市区2016年1月至11月连续60天的空气质量指数,制成如图所示的频率分布直方图.
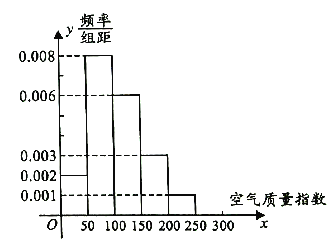
(1)求这60天中属轻度污染的天数;
(2)求这60天空气质量指数的平均值;
(3)一般地,当空气质量为轻度污染或轻度污染以上时才会出现雾霾天气,且此时出现雾霾天气的概率为![]() ,请根据统计数据,求在未来2天里,邵阳市恰有1天出现雾霾天气的概率.
,请根据统计数据,求在未来2天里,邵阳市恰有1天出现雾霾天气的概率.
