题目内容
【题目】已知函数![]() .
.
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)记函数![]() 的两个零点分别为
的两个零点分别为![]() ,且
,且![]() .已知
.已知![]() ,若不等式
,若不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)函数![]() 在
在![]() 上单调递增;在
上单调递增;在![]() 上单调递减; (Ⅱ)
上单调递减; (Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)求出函数的导数,通过讨论![]() 的范围,求出函数 的单调区间即可; (Ⅱ)分离参数得:
的范围,求出函数 的单调区间即可; (Ⅱ)分离参数得:![]() ,从而可得
,从而可得![]() 恒成立;再令
恒成立;再令![]() ,从而可得不等式
,从而可得不等式![]() 在
在![]() 上恒成立,再令
上恒成立,再令![]() ,从而利用导数化恒成立问题为最值问题即可.
,从而利用导数化恒成立问题为最值问题即可.
试题解析:(Ⅰ)依题意,函数![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
当![]() 时,
时,![]() 恒成立,故函数
恒成立,故函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,令
时,令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() ;
;
故函数![]() 在
在![]() 上单调递增;在
上单调递增;在![]() 上单调递减,
上单调递减,
(Ⅱ)由(I)可知![]() 分别为方程
分别为方程![]() 的两个根,即
的两个根,即![]() ,
,![]() ,
,
所以原式等价于![]() .
.
因为![]() ,
,![]() ,所以原式等价于
,所以原式等价于![]() ,
,
又由![]() ,
,![]() 作差得,
作差得,![]() ,即
,即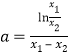 .
.
所以原式等价于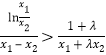 .
.
因为![]() ,原式恒成立,即
,原式恒成立,即![]() 恒成立.
恒成立.
令![]() ,则不等式
,则不等式![]() 在
在![]() 上恒成立.
上恒成立.
令![]() ,则
,则![]() ,
,
当![]() 时,可见
时,可见![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增,又
上单调递增,又![]() 在
在![]() 恒成立,符合题意;
恒成立,符合题意;
当![]() 时,可见当
时,可见当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 时单调递增,在
时单调递增,在![]() 时单调递减.
时单调递减.
又![]() ,所以
,所以![]() 在
在![]() 上不能恒小于0,不符合题意,舍去.
上不能恒小于0,不符合题意,舍去.
综上所述,若不等式![]() 恒成立,只须
恒成立,只须![]() ,又
,又![]() ,所以
,所以![]() .
.

【题目】《中华人民共和国个人所得税法》规定,公民全月工资所得不超过3500元的部分不必纳税,超过3500元的部分为全月应纳税所得额。此项税款按下表分段累计计算:
全月应纳税所得额 | 税率(%) |
不超过1500元的部分 | 3 |
超过1500元至4500元的部分 | 10 |
超过4500元至9000元的部分 | 20 |
(1)某人10月份应交此项税款为350元,则他10月份的工资收入是多少?
(2)假设某人的月收入为![]() 元,
元, ![]() ,记他应纳税为
,记他应纳税为![]() 元,求
元,求![]() 的函数解析式.
的函数解析式.
【题目】某DVD光盘销售部每天的房租、人员工资等固定成本为300元,每张DVD光盘的进价是6元,销售单价与日均销售量的关系如表所示:
销售单价(元) | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
日均销售量(张) | 480 | 440 | 400 | 360 | 320 | 280 | 240 |
(1)请根据以上数据作出分析,写出日均销售量P(x)(张)关于销售单价x(元)的函数关系式,并写出其定义域;
(2)问这个销售部销售的DVD光盘销售单价定为多少时才能使日均销售利润最大?最大销售利润是多少?
