题目内容
【题目】一座圆拱桥,当水面在如图所示位置时,拱顶离水面2米,水面宽12米,当水面下降1米后,水面宽多少米?
![]()
【答案】2![]()
【解析】试题分析; 建立适当的直角坐标系,得到相关各点的坐标,通过设圆的半径,可得圆的方程,然后将点的坐标代入确定圆的方程,设当水面下降1米后可设![]() 的坐标为
的坐标为![]() 根据点在圆上,可求得
根据点在圆上,可求得![]() 的值,从而得到问题的结果.
的值,从而得到问题的结果.
试题解析;以圆拱顶点为原点,以过圆拱顶点的竖直直线为y轴,建立如图所示的平面直角坐标系.
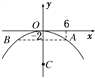
设圆心为C,水面所在弦的端点为A,B,则由已知可得A(6,-2),
设圆的半径长为r,则C(0,-r),即圆的方程为x2+(y+r)2=r2.将点A的坐标代入上述方程可得r=10,所以圆的方程为x2+(y+10)2=100.
当水面下降1米后,可设A′(x0,-3)(x0>0),代入x2+(y+10)2=100,解得2x0=2![]() ,即当水面下降1米后,水面宽2
,即当水面下降1米后,水面宽2![]() 米.
米.

练习册系列答案
相关题目
【题目】某DVD光盘销售部每天的房租、人员工资等固定成本为300元,每张DVD光盘的进价是6元,销售单价与日均销售量的关系如表所示:
销售单价(元) | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
日均销售量(张) | 480 | 440 | 400 | 360 | 320 | 280 | 240 |
(1)请根据以上数据作出分析,写出日均销售量P(x)(张)关于销售单价x(元)的函数关系式,并写出其定义域;
(2)问这个销售部销售的DVD光盘销售单价定为多少时才能使日均销售利润最大?最大销售利润是多少?