题目内容
过抛物线x2=2py(p>0)焦点的直线与抛物线交于不同的两点A、B,则抛物线上A、B两点处的切线斜率之积是( )
A.P2 B.-p2 C.-1 D.1
A.P2 B.-p2 C.-1 D.1
C
设A(x1,y1),B(x2,y2)
∵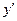 =
=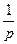 x,
x,
∴过A点的切线斜率为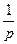 x1, 过B点的切线斜率为
x1, 过B点的切线斜率为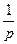 x2,
x2,
∴过抛物线上A、B两点处的切线斜率之积是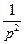 x1x2,
x1x2,
设过抛物线焦点的直线方程为y=kx+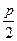 与x2=2py联立消去y得
与x2=2py联立消去y得
x2-2kpx-p2=0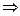 x1x2=-p2
x1x2=-p2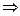
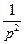 x1x2=-1.
x1x2=-1.
∵
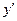 =
=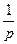 x,
x,∴过A点的切线斜率为
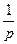 x1, 过B点的切线斜率为
x1, 过B点的切线斜率为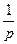 x2,
x2,∴过抛物线上A、B两点处的切线斜率之积是
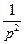 x1x2,
x1x2,设过抛物线焦点的直线方程为y=kx+
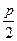 与x2=2py联立消去y得
与x2=2py联立消去y得x2-2kpx-p2=0
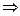 x1x2=-p2
x1x2=-p2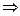
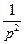 x1x2=-1.
x1x2=-1.
练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
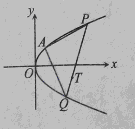
 ,求点A的坐标;
,求点A的坐标; 的焦点作直线交抛物线于
的焦点作直线交抛物线于 两点,线段
两点,线段 的中点
的中点 的纵坐标为2,则线段
的纵坐标为2,则线段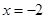 ,则抛物线的方程是( )
,则抛物线的方程是( )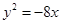
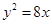
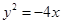
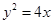
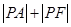 的最小值及此时P点的坐标.
的最小值及此时P点的坐标. 上的动点,点P在y轴上的射影是M,点A 的坐标是(4,a),则当
上的动点,点P在y轴上的射影是M,点A 的坐标是(4,a),则当 时,
时, 的最小值是( )
的最小值是( )



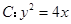 的焦点为
的焦点为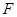 ,
,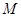 为抛物线
为抛物线 上一点,且点
上一点,且点 .
.