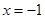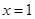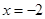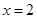题目内容
已知点A(3,2), 点P是抛物线y2=4x上的一个动点,F为抛物线的焦点,求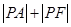 的最小值及此时P点的坐标.
的最小值及此时P点的坐标.
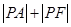 的最小值及此时P点的坐标.
的最小值及此时P点的坐标.4, (1,2).
试题分析:设点P在准线上的射影为D,由抛物线的定义把问题转化为求PA+PD的最小值,同时可推断出当D,P,A三点共线时PA+PD最小,答案可得.
设点P在准线上的射影为D,记抛物线y2=2x的焦点为F(1,0),准线l是x= -1,由抛物线的定义知点P到焦点F的距离等于它到准线l的距离,即PF=PD ,
因此PA +PF="PA+" PD
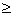 AD="4," 即当D,P,M三点共线时PA+PD最小,此时P(1,2).
AD="4," 即当D,P,M三点共线时PA+PD最小,此时P(1,2).
练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
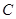 :
: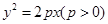 的焦点为
的焦点为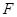 ,准线为
,准线为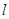 ,过准线
,过准线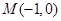 且斜率为
且斜率为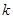 的直线
的直线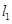 交抛物线
交抛物线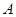 ,
,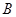 两点,线段
两点,线段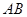 的中点为
的中点为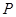 ,直线
,直线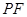 交抛物线
交抛物线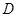 ,
,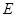 两点.
两点. 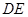 的中点?若存在,求出
的中点?若存在,求出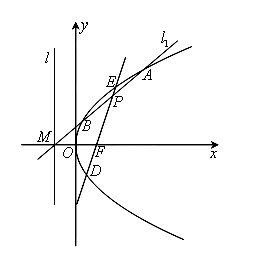
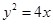 的准线方程为________.
的准线方程为________.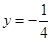
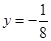
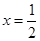
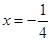
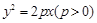 的焦点为
的焦点为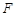 ,点
,点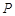 是抛物线上的一点,且其纵坐标为4,
是抛物线上的一点,且其纵坐标为4,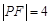 .
.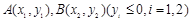 是抛物线上的两点,
是抛物线上的两点,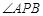 的角平分线与
的角平分线与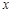 轴垂直,求
轴垂直,求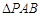 的面积最大时直线
的面积最大时直线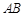 的方程.
的方程.
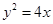 的准线方程是
的准线方程是