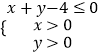题目内容
【题目】在直角坐标系![]() 中,已知圆
中,已知圆![]() 圆心为
圆心为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线与圆
的直线与圆![]() 相交于不同的两点
相交于不同的两点![]() 、
、![]() .
.
(![]() )求
)求![]() 的取值范围;
的取值范围;
(![]() )是否存在常数
)是否存在常数![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求
共线?如果存在,求![]() 值;如果不存在,请说明理由.
值;如果不存在,请说明理由.
【答案】(1)![]() ;(2)不存在.
;(2)不存在.
【解析】试题分析:(1)圆的方程可得圆心为![]() ,半径为2,圆的面积为
,半径为2,圆的面积为![]() ,设直线l的方程为y=kx+2.直线l与圆
,设直线l的方程为y=kx+2.直线l与圆![]() 交于两个不同的点A,B等价于
交于两个不同的点A,B等价于![]() <2,解不等式即可求出结果.(2)设
<2,解不等式即可求出结果.(2)设![]() ,则
,则![]() +
+![]() ,由
,由![]()
得![]() ,根据韦达定理和共线定理,即可解得
,根据韦达定理和共线定理,即可解得![]() .由(2)知
.由(2)知![]() ,故可判断
,故可判断![]() 的情况.
的情况.
试题解析:(1)圆的方程可化为![]() ,可得圆心为
,可得圆心为![]() ,半径为2,故圆的面积为
,半径为2,故圆的面积为![]() .
.
设直线l的方程为y=kx+2.直线l与圆![]() 交于两个不同的点A,B等价于
交于两个不同的点A,B等价于![]() <2,化简得
<2,化简得![]() ,解得
,解得![]() ,即k的取值范围为
,即k的取值范围为![]() .
.
(2)设![]() ,则
,则![]() +
+![]() =(x1+x2,y1+y2),由
=(x1+x2,y1+y2),由![]()
得![]() ,
,
解此方程得x1,2=![]() .
.
则![]() -
-![]() ,①
,①
又![]() .②
.②
而![]() ,
,![]() =(6,-2).
=(6,-2).
所以![]() +
+![]() 与
与![]() 共线等价于
共线等价于![]() ,将①②代入上式,解得
,将①②代入上式,解得![]() .由(2)知
.由(2)知![]() ,故没有符合题意的常数
,故没有符合题意的常数![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目