题目内容
【题目】已知等比数列{an}中,a1=64,公比q≠1,a2 , a3 , a4又分别是某个等差数列的第7项,第3项,第1项.
(1)求an;
(2)设bn=log2an , 求数列{|bn|}的前n项和Tn .
【答案】
(1)解:等比数列{an}中,a1=64,公比q≠1,
a2,a3,a4又分别是某个等差数列的第7项,第3项,第1项,
可得a2﹣a3=4d,a3﹣a4=2d,(d为某个等差数列的公差),
即有a2﹣a3=2(a3﹣a4),
即a2﹣3a3+2a4=0,
即为a1q﹣3a1q2+2a1q3=0,
即有1﹣3q+2q2=0,
解得q= ![]() (1舍去),
(1舍去),
则an=a1qn﹣1=64( ![]() )n﹣1=27﹣n;
)n﹣1=27﹣n;
(2)解:bn=log2an=log227﹣n=7﹣n,
设数列{bn}的前n项和Sn,
Sn= ![]() (6+7﹣n)n=
(6+7﹣n)n= ![]() n(13﹣n),
n(13﹣n),
当1≤n≤7时,前n项和Tn=Sn= ![]() n(13﹣n);
n(13﹣n);
当n≥8时,an<0,则前n项和Tn=﹣(Sn﹣S7)+S7=2S7﹣Sn=2× ![]() ×7×6﹣
×7×6﹣ ![]() n(13﹣n)
n(13﹣n)
= ![]() (n2﹣13n+84),
(n2﹣13n+84),
则前n项和Tn= 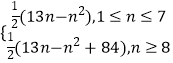 .
.
【解析】(1)运用等差数列的通项公式和等比数列的通项公式,可得公比的方程,求得q,进而得到an;(2)求得bn=log227﹣n=7﹣n,设数列{bn}的前n项和Sn , 运用等差数列的求和公式可得Sn , 讨论当1≤n≤7时,前n项和Tn=Sn;当n≥8时,an<0,则前n项和Tn=﹣(Sn﹣S7)+S7=2S7﹣Sn , 计算即可得到所求和.
【考点精析】利用数列的前n项和对题目进行判断即可得到答案,需要熟知数列{an}的前n项和sn与通项an的关系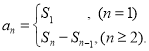 .
.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目