题目内容
【题目】设命题p:m∈{x|x2+(a﹣8)x﹣8a≤0},命题q:方程 ![]() =1表示焦点在x轴上的双曲线.
=1表示焦点在x轴上的双曲线.
(1)若当a=1时,命题p∧q假命题,p∨q”为真命题,求实数m的取值范围;
(2)若命题p是命题q的充分不必要条件,求实数a的取值范围.
【答案】
(1)解:a=1时,x2+(a﹣8)x﹣8a≤0,
即x2﹣7x﹣8≤0,解得:﹣1≤x≤8,
故p:﹣1≤m≤8,
若方程 ![]() =1表示焦点在x轴上的双曲线,
=1表示焦点在x轴上的双曲线,
则 ![]() ,解得:m>5
,解得:m>5
故q:m>5;
若命题p∧q假命题,p∨q”为真命题,
则p,q一真一假,
故 ![]() 或
或 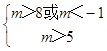 ,
,
解得:m∈[﹣1,5]∪(8,+∞)
(2)解:命题p:m∈{x|x2+(a﹣8)x﹣8a≤0}={x|(x﹣8)(x+a)≤0},
﹣a<8即a>﹣8时,p:[﹣a,8],
﹣a>8,即a<﹣8时,p:[8,﹣a],
q:m>5,
若命题p是命题q的充分不必要条件,
即[﹣a,8](5,+∞),或[8,﹣a](5,+∞),
故﹣a>5,解得:a<﹣5
【解析】(1)分别求出p,q为真时的m的范围,根据p,q一真一假,得到关于m的不等式组,解出即可;(2)通过讨论a的范围,得到关于m的不等式组,解出即可.
【考点精析】掌握复合命题的真假是解答本题的根本,需要知道“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真.

【题目】如图,在等腰直角△ABO中,设 ![]() =
= ![]() ,
, ![]() =
= ![]() ,|
,| ![]() |=|
|=| ![]() |=1,C为AB上靠近A点的三等分点,过C作AB的垂线l,设P为垂线上任一点,
|=1,C为AB上靠近A点的三等分点,过C作AB的垂线l,设P为垂线上任一点, ![]() =
= ![]() ,则
,则 ![]() (
( ![]() ﹣
﹣ ![]() )=( )
)=( ) 
A.![]()
B.﹣ ![]()
C.﹣ ![]()
D.![]()