Question

【题目】已知f（x）=（x2﹣2ax）ebx ， x为自变量．
（1）函数f（x）分别在x=﹣1和x=1处取得极小值和极大值，求a，b．
（2）若a≥0且b=1，f（x）在[﹣1，1]上是单调函数，求a的取值范围．

Answer 1

【答案】
（1）解：∵f（x）=（x2﹣2ax）ebx，

∴f'（x）=ebx[bx2+2（1﹣ab）x﹣2a]，

∵函数f（x）分别在x=﹣1和x=1处取得极小值和极大值，

∴﹣1，1是bx2+2（1﹣ab）x﹣2a=0的两个根，

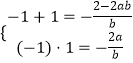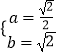∴ ，∴ 或 ，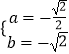

经检验，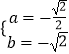

（2）解：f'（x）=ex[x2+2（1﹣a）x﹣2a]

①若f（x）在[﹣1，1]递减，则f'（x）≤0在[﹣1，1]恒成立，

∴只需x2+2（1﹣a）x﹣2a≤0在[﹣1，1]恒成立，

即2a（x+1）≥x2+2x在[﹣1，1]恒成立，

x=﹣1时2a（x+1）≥x2+2x在[﹣1，1]恒成立；

x∈（﹣1，1]时，需满足a≥ ，令g（x）= ，

则g′（x）= ＞0在x∈（﹣1，1]恒成立，

∴g（x）在（﹣1，1]递增，∴g（x）max=g（1）= ，∴a≥ ；

②若f（x）在[﹣1，1]递增，则f'（x）≥0在[﹣1，1]恒成立，

但f'（﹣1）=﹣1，∴f（x）在[﹣1，1]不递增；

综上a≥

【解析】（1）求导数，利用函数f（x）分别在x=﹣1和x=1处取得极小值和极大值，﹣1，1是bx2+2（1﹣ab）x﹣2a=0的两个根，即可得出结论；（2）先由f′（x）＞0，再根据函数f（x）在[﹣1，1]上为单调函数，将原问题转化为x2+2（1﹣a）x﹣2a≤0在[﹣1，1]恒成立问题，列出关于a的不等关系解之即得．
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识点，需要掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减；求函数在上的最大值与最小值的步骤：（1）求函数在内的极值；（2）将函数的各极值与端点处的函数值，比较，其中最大的是一个最大值，最小的是最小值才能正确解答此题．