题目内容
已知抛物线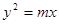
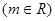 的焦点为
的焦点为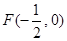 ,过点
,过点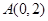 的直线
的直线 与抛物线
与抛物线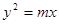 有且只有一个公共点,求直线
有且只有一个公共点,求直线 的方程。
的方程。
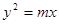
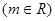 的焦点为
的焦点为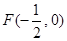 ,过点
,过点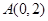 的直线
的直线 与抛物线
与抛物线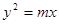 有且只有一个公共点,求直线
有且只有一个公共点,求直线 的方程。
的方程。由已知得,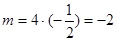 ,
,
所以抛物线和方程是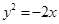 ……………………3分
……………………3分
⑴ 当直线 的斜率不存在时,
的斜率不存在时,
直线 的方程为
的方程为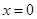 ,直线
,直线 与抛物线
与抛物线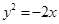 切于点(0,0) ……5分
切于点(0,0) ……5分
⑵ 当直线 斜率存在时,设直线
斜率存在时,设直线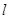 的斜率为
的斜率为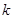 ,直线
,直线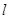 方程为
方程为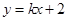 ,
,
代入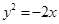 得:
得: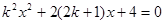 。 …………………………7分
。 …………………………7分
① 当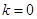 时,
时,
直线 的方程为
的方程为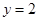 ,
,
 的方程与抛物线
的方程与抛物线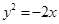 有且只有一个公共点(-2,2) ………9分
有且只有一个公共点(-2,2) ………9分
②当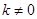 时,
时,
由△=0得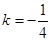 ,则直线
,则直线 的方程:
的方程: …………11分
…………11分
综上所述:所求直线 的方程为
的方程为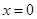 和
和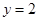 及
及 。
。
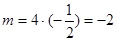 ,
,所以抛物线和方程是
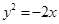 ……………………3分
……………………3分⑴ 当直线
 的斜率不存在时,
的斜率不存在时,直线
 的方程为
的方程为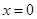 ,直线
,直线 与抛物线
与抛物线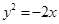 切于点(0,0) ……5分
切于点(0,0) ……5分⑵ 当直线
 斜率存在时,设直线
斜率存在时,设直线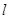 的斜率为
的斜率为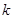 ,直线
,直线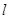 方程为
方程为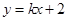 ,
,代入
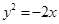 得:
得: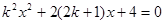 。 …………………………7分
。 …………………………7分① 当
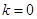 时,
时,直线
 的方程为
的方程为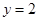 ,
, 的方程与抛物线
的方程与抛物线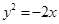 有且只有一个公共点(-2,2) ………9分
有且只有一个公共点(-2,2) ………9分②当
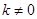 时,
时,由△=0得
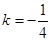 ,则直线
,则直线 的方程:
的方程: …………11分
…………11分综上所述:所求直线
 的方程为
的方程为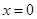 和
和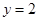 及
及 。
。略

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
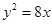 的焦点为
的焦点为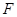 ,准线为
,准线为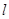 ,
,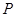 为抛物线上一点,
为抛物线上一点,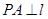 ,
,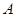 为垂足.如果直线
为垂足.如果直线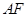 的斜率为
的斜率为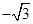 ,那么
,那么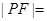
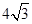
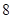
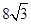
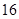
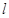 过抛物线
过抛物线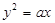 的焦点F,且与
的焦点F,且与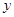 轴相交于点A,若
轴相交于点A,若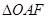
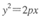 的焦点为F,点A、B、C在此抛物线上,点A坐标为(1, 2).若点F恰为
的焦点为F,点A、B、C在此抛物线上,点A坐标为(1, 2).若点F恰为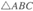 的重心,则直线BC的方程为
的重心,则直线BC的方程为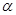 的直线经过抛物线
的直线经过抛物线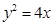 的焦点,且与抛物线交于A、B两点,Q为A、B中点,
的焦点,且与抛物线交于A、B两点,Q为A、B中点,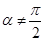 ,作线段AB的垂直平分线
,作线段AB的垂直平分线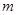 交x轴于点P,证明:|AB|=2|PF|。
交x轴于点P,证明:|AB|=2|PF|。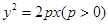 的焦点F的直线AB交抛物线于A,B两点,弦AB的中点为M,过M作AB的垂直平分线交x轴于N,
的焦点F的直线AB交抛物线于A,B两点,弦AB的中点为M,过M作AB的垂直平分线交x轴于N,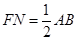
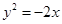 的焦点坐标是________
的焦点坐标是________ 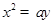 过点
过点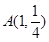 ,则点
,则点 到此抛物线的焦点的距离为 .
到此抛物线的焦点的距离为 .