题目内容
(本题13分)
已知等比数列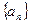 的前
的前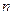 项和是
项和是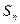 ,满足
,满足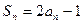 .
.
(Ⅰ)求数列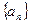 的通项
的通项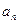 及前
及前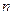 项和
项和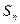 ;
;
(Ⅱ)若 数列
数列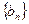 满足
满足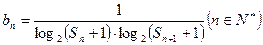 ,求数列
,求数列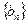 的前
的前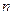 项和
项和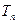 ;
;
(Ⅲ)若对任意的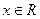 ,恒有
,恒有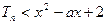 成立,求实数
成立,求实数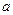 的取值范围.
的取值范围.
已知等比数列
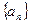 的前
的前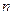 项和是
项和是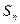 ,满足
,满足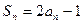 .
.(Ⅰ)求数列
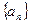 的通项
的通项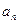 及前
及前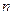 项和
项和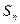 ;
;(Ⅱ)若
 数列
数列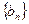 满足
满足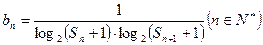 ,求数列
,求数列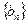 的前
的前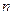 项和
项和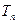 ;
;(Ⅲ)若对任意的
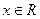 ,恒有
,恒有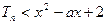 成立,求实数
成立,求实数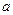 的取值范围.
的取值范围.解: (I)由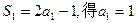 ,
,
由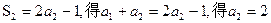 …………1分
…………1分
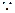 数列
数列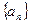 是等比数列
是等比数列 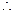 数列
数列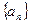 的公比
的公比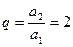
所以,数列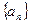 的通项公
的通项公 式为
式为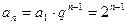
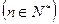 …………3分
…………3分
前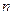 项和公式为
项和公式为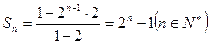 . ………………………4分
. ………………………4分
(II)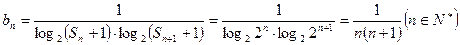
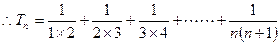 ……………………………6分
……………………………6分
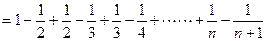 ………………………8分
………………………8分
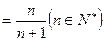 …………………………………………9分
…………………………………………9分
(Ⅲ)由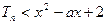 恒成立 即
恒成立 即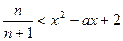 恒成立
恒成立
即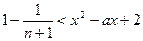 恒成立 ……………………………………10分
恒成立 ……………………………………10分
必须且只须满足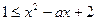 恒成立 ………………………………11分
恒成立 ………………………………11分
即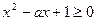 在R上恒成立
在R上恒成立 
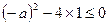 ,………………12分
,………………12分
解得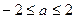 . …………………………………………13分
. …………………………………………13分
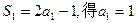 ,
,由
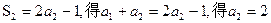 …………1分
…………1分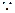 数列
数列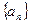 是等比数列
是等比数列 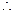 数列
数列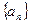 的公比
的公比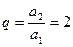
所以,数列
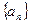 的通项公
的通项公 式为
式为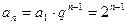
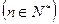 …………3分
…………3分前
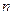 项和公式为
项和公式为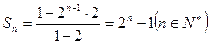 . ………………………4分
. ………………………4分(II)
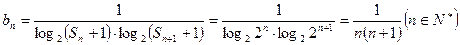
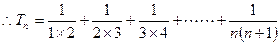 ……………………………6分
……………………………6分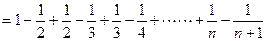 ………………………8分
………………………8分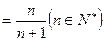 …………………………………………9分
…………………………………………9分(Ⅲ)由
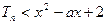 恒成立 即
恒成立 即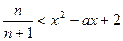 恒成立
恒成立即
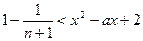 恒成立 ……………………………………10分
恒成立 ……………………………………10分必须且只须满足
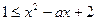 恒成立 ………………………………11分
恒成立 ………………………………11分即
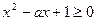 在R上恒成立
在R上恒成立 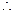
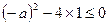 ,………………12分
,………………12分解得
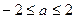 . …………………………………………13分
. …………………………………………13分略

练习册系列答案
相关题目
 是正项等比数列,满足
是正项等比数列,满足
 的通项公式;
的通项公式; 是否存在正整数
是否存在正整数 ,使得对一切
,使得对一切 恒成立,若存在,请求出M的最小值;若不存在,请说明理由。
恒成立,若存在,请求出M的最小值;若不存在,请说明理由。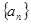 为等差数列,若
为等差数列,若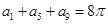 ,则
,则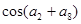 的值为
的值为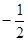
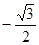
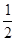

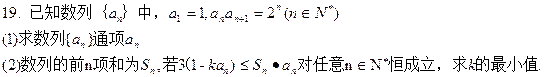
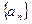 满足
满足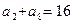 ,则
,则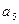 等于( )
等于( )
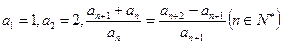
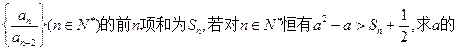 取值范围.
取值范围.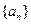 满足
满足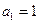 ,
,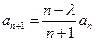 ,其中
,其中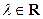 ,
,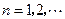 .给出下列命题:
.给出下列命题: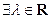 ,对于任意
,对于任意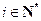 ,
,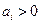 ;
;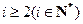 ,
,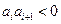 ;
;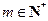 ,当
,当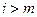 (
(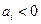 .
.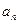 }的前
}的前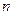 项和
项和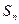 ,对于任意
,对于任意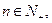 点
点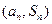 都在函数
都在函数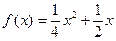 的图象上.
的图象上. 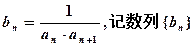 的前n项和为
的前n项和为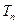 ,求
,求