题目内容
【题目】如图,在直四棱柱![]() 中,已知
中,已知![]() ,
,![]() .
.
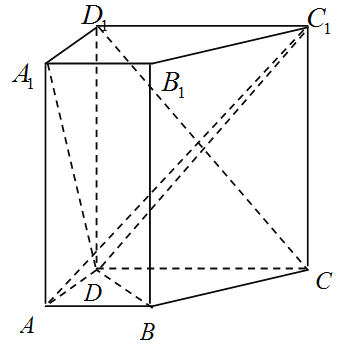
(1)求证:![]() ;
;
(2)设![]() 是
是![]() 上一点,试确定
上一点,试确定![]() 的位置,使
的位置,使![]() 平面
平面![]() ,并说明理由.
,并说明理由.
【答案】⑴连DC1,正方形DD1C1C中,D1C⊥C1D
∵AD⊥平面DD1C1C ∴AD⊥CD1又AD∩CD1=D
∴CD1⊥平面DA C1![]()
⑵ E 为AC中点时,![]() 平面
平面![]() 9’
9’
梯形ABCD中,DE∥且=" AB " ∴AD∥且=BE
∵AD∥且= A1D1∴A1D1∥且="BE " ∴A1D1EB是平行四边形
∴D1E∥B A1又B A1![]() 平面DB A1D1E
平面DB A1D1E![]() 平面DB A1
平面DB A1
∴![]() 平面
平面![]()
【解析】试题分析:
(1)本题为证线与线垂直,常规思路为转化为证线与另一条
直线所在的平面垂直。结合条件,可证出![]() 平面
平面![]() ,则得:
,则得:![]() .
.
(2)本题为通过确定点![]() 的位置来证明证线与面平行,可通过题中的条件进行大胆设想,(
的位置来证明证线与面平行,可通过题中的条件进行大胆设想,(![]() 为中点),然后进行对应的证明,可解决;
为中点),然后进行对应的证明,可解决;
试题解析:
(1)在直四棱柱![]() 中,
中,
连结![]() ,
,![]() ,
,![]() 四边形
四边形![]() 是正方形.
是正方形.![]() .
.
又![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() .
.![]() 平面
平面![]() ,且
,且![]() ,
,
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,![]() .
.

(2)连结![]() ,连结
,连结![]() ,设
,设![]() ,
,
![]() ,连结
,连结![]() ,
,![]() 平面
平面![]() 平面
平面![]() ,
,
要使![]() 平面
平面![]() ,须使
,须使![]() ,
,
又![]() 是
是![]() 的中点.
的中点.![]() 是
是![]() 的中点.
的中点.
又易知![]() ,
,![]() .
.
即![]() 是
是![]() 的中点.综上所述,当
的中点.综上所述,当![]() 是
是![]() 的中点时,可使
的中点时,可使![]() 平面
平面![]() .
.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案【题目】大学先修课程,是在高中开设的具有大学水平的课程,旨在让学有余力的高中生早接受大学思维方式、学习方法的训练,为大学学习乃至未来的职业生涯做好准备.某高中成功开设大学先修课程已有两年,共有250人参与学习先修课程,这两年学习先修课程的学生都参加了高校的自主招生考试(满分100分),结果如下表所示:
分数 |
|
|
|
|
|
人数 | 25 | 50 | 100 | 50 | 25 |
参加自主招生获得通过的概率 | 0.9 | 0.8 | 0.6 | 0.4 | 0.3 |
(Ⅰ)这两年学校共培养出优等生150人,根据下图等高条形图,填写相应列联表,并根据列联表检验能否在犯错的概率不超过0.01的前提下认为学习先修课程与优等生有关系?

优等生 | 非优等生 | 总计 | |
学习大学先修课程 | 250 | ||
没有学习大学先修课程 | |||
总计 | 150 |
(Ⅱ)已知今年全校有150名学生报名学习大学选项课程,并都参加了高校的自主招生考试,以前两年参加大学先修课程学习成绩的频率作为今年参加大学先修课程学习成绩的概率.
(ⅰ)在今年参与大学先修课程学习的学生中任取一人,求他获得高校自主招生通过的概率;
(ⅱ)某班有4名学生参加了大学先修课程的学习,设获得高校自主招生通过的人数为![]() ,求
,求![]() 的分布列,试估计今年全校参加大学先修课程学习的学生获得高校自主招生通过的人数.
的分布列,试估计今年全校参加大学先修课程学习的学生获得高校自主招生通过的人数.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式:![]() ,其中
,其中![]()
