题目内容
在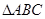 中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D。
中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D。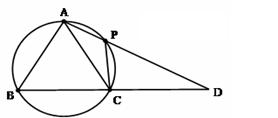
(1)求证: 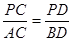 ;
;
(2)若AC=3,求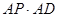 的值。
的值。
(1)主要是利用圆的内接四边形的性质,结合相似来证明。
(2)根据△PAB~BAD 的相似来得到长度的求解。
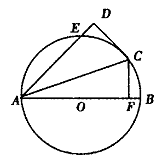
解析试题分析:(1) 证明:连结BP,∵四边形ABCP内接于圆,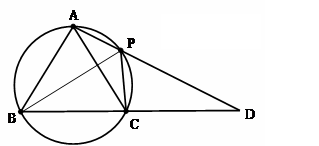
∴∠PCD=∠BAD 又∠PDC=∠BDA
∴△PCD~△BAD
∴
又∵AB=AC
∴ (5分)
(5分)
(2)连结BP。∵AB=AC,∴∠ABC=∠ACB
又∵四边形ABCP内接于圆 ∴∠ACB=∠APB
从而∠ABC=∠APB 又∠BAP=∠BAD
∴△PAB~BAD ∴ ∴
∴
又∵AB=AC=3 ∴ =
= (10分)
(10分)
考点:平面几何中圆的性质运用
点评:主要是考查了相似三角形以及圆内的几何性质的运用,属于基础题。

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
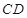 为△
为△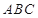 外接圆的切线,
外接圆的切线,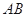 的延长线交直线
的延长线交直线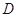 ,
,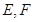 分别为弦
分别为弦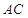 上的点,且
上的点,且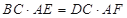 ,
,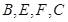 四点共圆.
四点共圆. 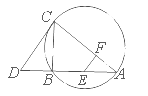
 是△
是△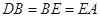 ,求过
,求过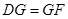 。求证:
。求证:

 AE=DC
AE=DC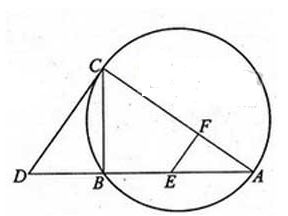

 ,
, ,
,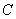 ,
, 四点共圆,
四点共圆,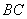 与
与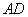 的延长线交于点
的延长线交于点 ,点
,点 在
在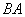 的延长线上.
的延长线上.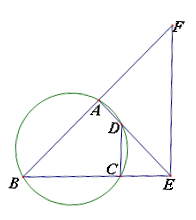
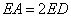 ,
, ,求
,求 的值;
的值;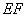 ∥
∥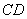 ,求证:线段
,求证:线段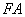 ,
,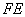 ,
, 成等比数列.
成等比数列.
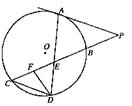
 是边长为
是边长为 的正方形,以
的正方形,以 为圆心,
为圆心,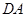 为半径的圆弧与以
为半径的圆弧与以 为直径的半圆
为直径的半圆 交于点
交于点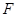 ,延长
,延长 交
交 于
于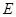 .
.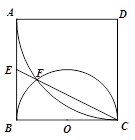
 的长.
的长.