题目内容
如图,AB是圆O的直径,C,D是圆O上两点,AC与BD相交于点E,GC,GD是圆O的切线,点F在DG的延长线上,且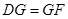 。求证:
。求证:
(Ⅰ)D、E、C、F四点共圆; (Ⅱ)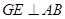

(Ⅰ)详见解析;(Ⅱ)详见解析.
解析试题分析:(Ⅰ)依据已知条件寻求出∠DGC、∠F、∠CAB+∠DBA的关系,借助对角互补证明D,E,C,F四点共圆;(Ⅱ)结合(Ⅰ)的结果进一步得到点G是经过D,E,C,F四点的圆的圆心,所以∠GCE=∠GEC,延长GE,继而证明∠AEH+∠CAB=90°即可.
试题解析:(Ⅰ)如图,连结OC,OD,则OC⊥CG,OD⊥DG,
设∠CAB=∠1,∠DBA=∠2,∠ACO=∠3,
则∠COB=2∠1,∠DOA=2∠2.
所以∠DGC=180°-∠DOC=2(∠1+∠2).
因为∠DGC=2∠F,所以∠F=∠1+∠2.
又因为∠DEC=∠AEB=180°-(∠1+∠2),
所以∠DEC+∠F=180°,所以D,E,C,F四点共圆.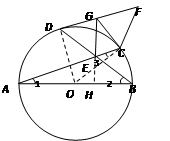
(Ⅱ)延长GE交AB于H.
因为GD=GC=GF,所以点G是经过D,E,C,F四点的圆的圆心.
所以GE=GC,所以∠GCE=∠GEC.
又因为∠GCE+∠3=90°,∠1=∠3,
所以∠GEC+∠3=90°,所以∠AEH+∠1=90°,
所以∠EHA=90°,即GE⊥AB.
考点:1、四点共圆;2、圆的切线的性质.

练习册系列答案
相关题目
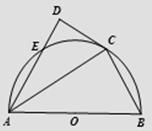
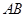 为半圆
为半圆 的直径,
的直径,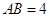 ,
, 为半圆上一点,过点
为半圆上一点,过点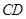 ,过点
,过点 作
作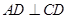 于
于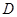 ,交圆于点
,交圆于点 ,
,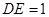 .
.
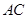 平分
平分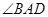 ;
; 的长.
的长.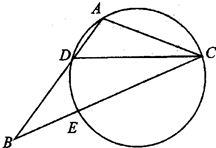
 是
是 的直径,弦
的直径,弦 与
与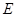 ,点
,点 为弦
为弦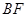 、
、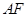 并延长交
并延长交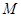 、
、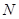 .
. 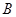 、
、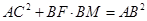 .
.
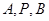 在
在 上,
上,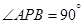 ,
,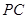 平分
平分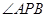 ,交
,交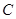 .求证:
.求证: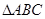 为等腰直角三角形.
为等腰直角三角形.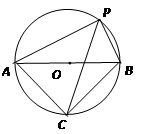
 是圆的内接四边形,
是圆的内接四边形, ,过
,过 点的圆的切线与
点的圆的切线与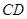 的延长线交于
的延长线交于 点,证明:
点,证明: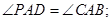
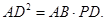
 均在⊙O上,且
均在⊙O上,且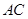 为⊙O的直径。
为⊙O的直径。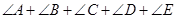 的值;
的值;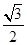 ,
, 与
与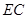 交于点
交于点 ,且
,且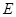 、
、 为弧
为弧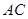 的三等分点,求
的三等分点,求 的长.
的长.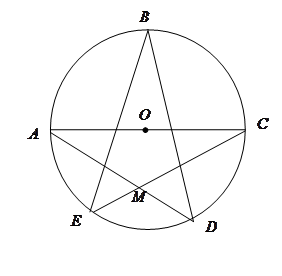
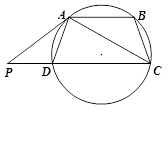
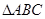 中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D。
中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D。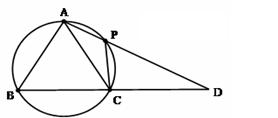
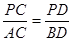 ;
;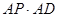 的值。
的值。
 ;
;