题目内容
已知:如右图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE,交BA的延长线于点E.求证:(1)△ABC≌△DCB (2)DE·DC=AE·BD.
(1)根据梯形为等腰梯形推断出∠ABC=∠DCB,同时根据AB=CD,BC=CB,证明出△ABC≌△DCB.
(2)根据(1)中△ABC≌△DCB推断出∠ACB=∠DBC,同时根据AD∥BC和ED∥AC推断出∠EDA=∠DBC,∠EAD=∠DCB,进而根据相似三角形判定定理推断出△ADE∽△CBD,进而根据相似三角形的性质求得DE:BD=AE:CD,推断出DE•DC=AE•BD.
解析试题分析:证明:(1) ∵四边形ABCD是等腰梯形,∴AC=DB
∵AB=DC,BC=CB,∴△ABC≌△BCD
(2)∵△ABC≌△BCD,∴∠ACB=∠DBC,∠ABC=∠DCB
∵AD∥BC,∴∠DAC=∠ACB,∠EAD=∠ABC
∵ED∥AC,∴∠EDA=∠DAC ∴∠EDA=∠DBC,∠EAD=∠DCB
∴△ADE∽△CBD ∴DE:BD=AE:CD, ∴DE·DC=AE·BD.
考点:相似三角形
点评:本题主要考查了相似三角形的判定.考查了学生对基础知识的熟练掌握.

练习册系列答案
相关题目
 为
为 的
的 边上一点,
边上一点, 经过点
经过点 ,交
,交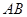 于另一点
于另一点 ,
, 经过点
经过点 ,
, 于另一点
于另一点 ,
, .
.
 四点共圆;
四点共圆; 切
切 .
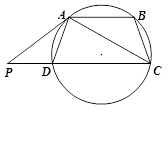
. 是圆的内接四边形,
是圆的内接四边形, ,过
,过 点的圆的切线与
点的圆的切线与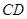 的延长线交于
的延长线交于 点,证明:
点,证明: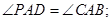
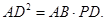
 、
、 分别与圆
分别与圆 相切于
相切于 、
、 ,
, 经过圆心
经过圆心 ,求证:
,求证: .
.
 中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D。
中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D。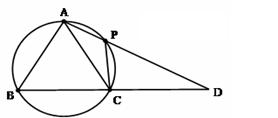
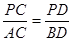 ;
;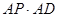 的值。
的值。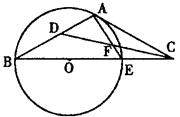
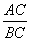 的值.
的值.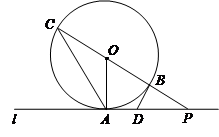
 (1)判断直线DB与⊙O的位置关系,并说明理由;
(1)判断直线DB与⊙O的位置关系,并说明理由;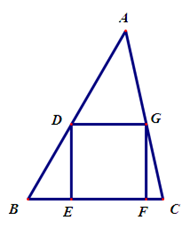
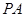 与⊙
与⊙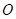 相切,
相切,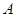 为切点,
为切点,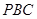 为割线,
为割线,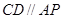 ,
,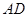 、
、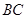 相交于
相交于 点,
点,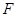 为
为 上一点,且
上一点,且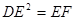 ·
·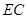 .
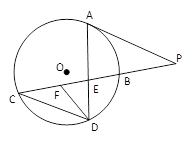
.
 ;
;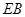 =
= ·
·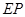 .
.