题目内容
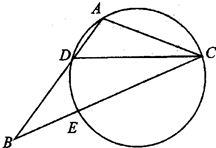
如图,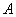 ,
, ,
,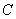 ,
, 四点共圆,
四点共圆,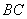 与
与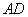 的延长线交于点
的延长线交于点 ,点
,点 在
在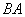 的延长线上.
的延长线上.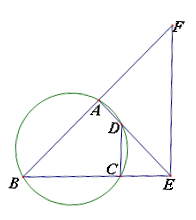
(1)若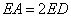 ,
, ,求
,求 的值;
的值;
(2)若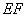 ∥
∥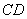 ,求证:线段
,求证:线段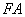 ,
,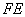 ,
, 成等比数列.
成等比数列.
(1) (2)先证
(2)先证 ∽
∽
解析试题分析:(Ⅰ)解:由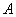 ,
, ,
,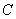 ,
, 四点共圆,得
四点共圆,得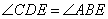 ,
,
又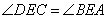 ,∴
,∴ 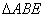 ∽
∽ ,于是
,于是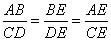 . ①
. ①
设 ,
,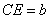 ,则由
,则由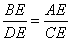 ,得
,得 ,即
,即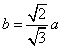
代入①,得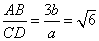 .
.
(Ⅱ)证明:由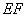 ∥
∥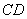 ,得
,得 .
.
∵ 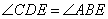 ,∴
,∴ 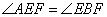 .又
.又 ,
,
∴  ∽
∽ ,于是
,于是 ,故
,故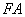 ,
,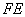 ,
, 成等比数列.
成等比数列.
考点:圆內接多边形的性质与判定;相似三角形的判定;相似三角形的性质.
点评:本题在圆内接四边形的条件下,一方面证明两条直线平行,另一方面求线段的比值.着重考查了圆中的比例线段、圆内接四边形的性质和相似三角形的判定与性质等知识点,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
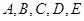 均在⊙O上,且
均在⊙O上,且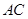 为⊙O的直径。
为⊙O的直径。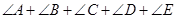 的值;
的值;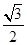 ,
, 与
与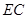 交于点
交于点 ,且
,且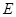 、
、 为弧
为弧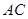 的三等分点,求
的三等分点,求 的长.
的长.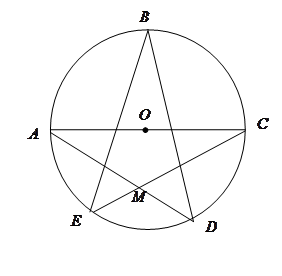
 中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D。
中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D。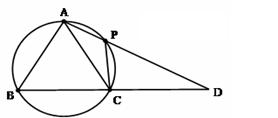
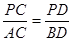 ;
;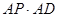 的值。
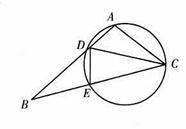
的值。 是圆内接四边形,延长
是圆内接四边形,延长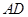 与的延长线
与的延长线 交于点
交于点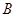 ,且
,且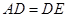 ,
, 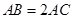 .
.
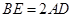 ;
;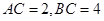 时,求
时,求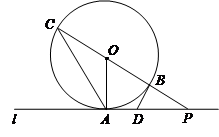
 (1)判断直线DB与⊙O的位置关系,并说明理由;
(1)判断直线DB与⊙O的位置关系,并说明理由; 是圆
是圆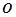 的直径,
的直径,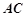 是弦,
是弦, ,垂足为
,垂足为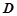 ,
,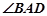 。
。
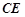 与圆
与圆 。
。
 ;
; 中,
中, ,
,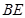 平分
平分 交
交 于点
于点 ,点
,点 在
在 上,
上, .
.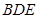 的外接圆的切线;
的外接圆的切线;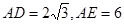 ,求
,求 的长.
的长.