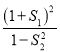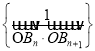题目内容
【题目】已知两点![]() 、
、![]() ,动点
,动点![]() 满足
满足![]() ,记
,记![]() 的轨迹为曲线
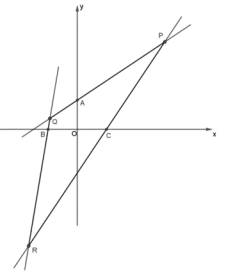
的轨迹为曲线![]() ,直线
,直线![]() (
(![]() )交曲线
)交曲线![]() 于
于![]() 、
、![]() 两点,点
两点,点![]() 在第一象限,
在第一象限,![]() 轴,垂足为
轴,垂足为![]() ,连结
,连结![]() 并延长交曲线
并延长交曲线![]() 于点
于点![]() .
.
(1)求曲线![]() 的方程,并说明曲线
的方程,并说明曲线![]() 是什么曲线;
是什么曲线;
(2)若![]() ,求△
,求△![]() 的面积;
的面积;
(3)证明:△![]() 为直角三角形.
为直角三角形.
【答案】(1)![]() ,轨迹是以
,轨迹是以![]() 、
、![]() 为焦点的椭圆;(2)
为焦点的椭圆;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)![]() ,根据椭圆定义,即可求出方程;
,根据椭圆定义,即可求出方程;
(2)设![]() ,可得
,可得![]() ,求出
,求出![]() 方程,与椭圆方程联立求出
方程,与椭圆方程联立求出![]() 点坐标,再将
点坐标,再将![]() 与椭圆方程联立,求出
与椭圆方程联立,求出![]() 坐标,即可求解;
坐标,即可求解;
(2)根据(2)中![]() 点坐标求出
点坐标求出![]() 斜率,即可证明结论.
斜率,即可证明结论.
(1)![]() ,
,
![]() 点轨迹就是以
点轨迹就是以![]() 为焦点的椭圆,
为焦点的椭圆,
其方程为![]() ;
;
(2)设![]() ,则
,则![]() ,
,
直线![]() 方程为
方程为![]() ,
,
联立 消去
消去![]() 得,
得,
![]() ,①
,①
设![]() 为方程①的解,
为方程①的解,
![]() ,
,
![]() ,
,
联立![]() ,解得
,解得![]() 或
或 ,
,
![]() ,
,
![]() ;
;
(3)由(2)得![]() ,
,
 ,
,
![]() ,即△
,即△![]() 为直角三角形.
为直角三角形.

练习册系列答案
相关题目
【题目】为了解儿子身高与其父亲身高的关系,随机调查了5对父子的身高,统计数据如下表所示.
编 号 | A | B | C | D | E |
父亲身高 | 174 | 176 | 176 | 176 | 178 |
儿子身高 | 175 | 175 | 176 | 177 | 177 |
(1)从这五对父子任意选取两对,用编号表示出所有可能取得的结果,并求随机事件![]() “两对父子中儿子的身高都不低于父亲的身高”发生的概率;
“两对父子中儿子的身高都不低于父亲的身高”发生的概率;
(2)由表中数据,利用“最小二乘法”求![]() 关于
关于![]() 的回归直线的方程.
的回归直线的方程.
参考公式: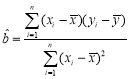 ,
,![]() ;回归直线:
;回归直线:![]() .
.