题目内容
【题目】已知点P和非零实数![]() ,若两条不同的直线
,若两条不同的直线![]() 均过点P,且斜率之积为
均过点P,且斜率之积为![]() ,则称直线
,则称直线![]() 是一组“
是一组“![]() 共轭线对”,如直
共轭线对”,如直![]() 是一组“
是一组“![]() 共轭线对”,其中O是坐标原点.
共轭线对”,其中O是坐标原点.
(1)已知![]() 是一组“
是一组“![]() 共轭线对”,求
共轭线对”,求![]() 的夹角的最小值;
的夹角的最小值;
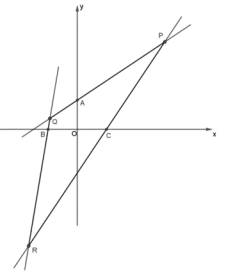
(2)已知点A(0,1)、点![]() 和点C(1,0)分别是三条直线PQ,QR,RP上的点(A,B,C与P,Q,R均不重合),且直线PR,PQ是“
和点C(1,0)分别是三条直线PQ,QR,RP上的点(A,B,C与P,Q,R均不重合),且直线PR,PQ是“![]() 共轭线对”,直线QP,QR是“
共轭线对”,直线QP,QR是“![]() 共轭线对”,直线RP,RQ是“
共轭线对”,直线RP,RQ是“![]() 共轭线对”,求点P的坐标;
共轭线对”,求点P的坐标;
(3)已知点![]() ,直线
,直线![]() 是“
是“![]() 共轭线对”,当
共轭线对”,当![]() 的斜率变化时,求原点O到直线
的斜率变化时,求原点O到直线![]() 的距离之积的取值范围.
的距离之积的取值范围.
【答案】(1)最小值为![]() ;(2)P(3,3)或
;(2)P(3,3)或![]() ;(3)
;(3)![]() .
.
【解析】
(1)设l1的斜率为k,则l2的斜率为![]() ,两直线的夹角为α,利用夹角公式及基本不等式求最值,即可得到l1,l2的夹角的最小值;
,两直线的夹角为α,利用夹角公式及基本不等式求最值,即可得到l1,l2的夹角的最小值;
(2)设直线PR,PQ,QR的斜率分别为k1,k2,k3,可得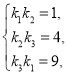 ,求解可得k1,k2,k3的值,进一步得到直线PR与直线PQ的方程,联立得P的坐标;
,求解可得k1,k2,k3的值,进一步得到直线PR与直线PQ的方程,联立得P的坐标;
(3)设l1:![]() ,
,![]() ,其中k≠0,利用两点间的距离公式可得原点O到直线l1,l2的距离,变形后利用基本不等式求解.
,其中k≠0,利用两点间的距离公式可得原点O到直线l1,l2的距离,变形后利用基本不等式求解.
(1)设![]() 的斜率为k,则
的斜率为k,则![]() 的斜率为
的斜率为![]() ,两直线的夹角为a,
,两直线的夹角为a,
则 ,
,
等号成立的条件是![]() ,所以最小值为
,所以最小值为![]() ;
;
(2)设直线![]() 的斜率分别为
的斜率分别为![]() ,
,
则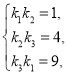 得
得![]() 或
或![]() .
.
当![]() 时,直线
时,直线![]() 的方程为y=
的方程为y=![]() ,直线
,直线![]() 的方程为y=
的方程为y=![]() ,联立得,P(3,3);
,联立得,P(3,3);
当![]() 时,,直线
时,,直线![]() 的方程为y=
的方程为y=![]() ,直线
,直线![]() 的方程为y=-
的方程为y=-![]() ,联立得,
,联立得,![]() ;
;
故所求为P(3,3)或![]() ;
;
(3)设![]() ,
,![]() ,其中k
,其中k![]() ,
,
故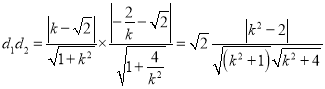 =
=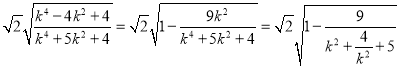
由于![]() (等号成立的条件是
(等号成立的条件是![]() ),故
),故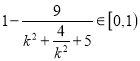 ,
,![]() .
.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案【题目】某企业生产A、B两种产品,生产每一吨产品所需的劳动力和煤、电耗如下表:
产品品种 | 劳动力 | 煤 | 电 |
A产品 | 3 | 9 | 4 |
B产品 | 10 | 4 | 5 |
已知生产每吨A产品的利润是7万元,生产每吨B产品的利润是12万元,现在条件有限,该企业仅有劳动力300个,煤360吨,并且供电局只能供电200千瓦,试问:该企业生产A、B两种产品各多少吨,才能获得最大利润?并求出最大利润.

