题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)是否存在实数![]() ,使得“对任意
,使得“对任意![]() 恒成立”?若存在,求出
恒成立”?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(1)答案不唯一,具体见解析(2)存在;实数![]() 的取值范围是
的取值范围是![]()
【解析】
![]() 对函数
对函数![]() 进行求导,分
进行求导,分![]() 和
和![]() 两种情况分别利用导数
两种情况分别利用导数![]() 判断函数
判断函数![]() 的单调性即可;
的单调性即可;
![]() 假设存在实数
假设存在实数![]() ,使得“
,使得“![]() 恒成立”,对函数
恒成立”,对函数![]() 进行求导,分
进行求导,分![]() 和
和![]() 两种情况判断函数
两种情况判断函数![]() 在
在![]() 上的单调性并判断函数
上的单调性并判断函数![]() 在
在![]() 上的最小值是否为非负.
上的最小值是否为非负.
(1)由题意知,![]() ,
,
则![]() ,
,
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,令
时,令![]() ,得
,得![]() ,
,
所以当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递增;
上单调递增;
(2)假设存在实数![]() ,使得“
,使得“![]() 恒成立”,
恒成立”,
因为函数![]() ,所以
,所以![]() ,
,
因为![]() ,
,
所以当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上恒成立,
上恒成立,
所以函数![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,
,
所以当![]() 时,对于任意
时,对于任意![]() ,有
,有![]() 恒成立;
恒成立;
当![]() ,即
,即![]() 时,令
时,令![]() ,得
,得![]() ,
,
解得![]()
![]() (其中
(其中![]() ),
),
所以![]() ,
,
所以函数![]() 在
在![]() 上单调递减,
上单调递减,
又![]() ,所以当
,所以当![]() 不符合题意,
不符合题意,
综上可知,存在实数![]() 使得“对任意
使得“对任意![]() 恒成立”,
恒成立”,
符合题意的实数![]() 的取值范围为
的取值范围为![]() .
.

 阅读快车系列答案
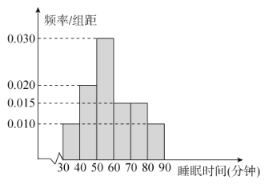
阅读快车系列答案【题目】全世界越来越关注环境保护问题,某监测站点于2018年1月某日起连续![]() 天监测空气质量指数(
天监测空气质量指数(![]() ),数据统计如下:
),数据统计如下:
空气质量指数( |
|
|
|
|
|
空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
天数 | 20 | 40 |
| 10 | 5 |
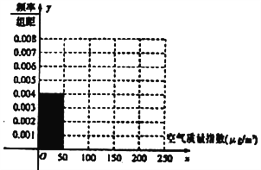
(1)根据所给统计表和频率分布直方图中的信息求出![]() ,
,![]() 的值,并完成频率分布直方图;
的值,并完成频率分布直方图;
(2)由频率分布直方图,求该组数据的众数和中位数;
(3)在空气质量指数分别属于![]() 和
和![]() 的监测数据中,用分层抽样的方法抽取
的监测数据中,用分层抽样的方法抽取![]() 天,再从中任意选取
天,再从中任意选取![]() 天,求事件
天,求事件![]() “两天空气都为良”发生的概率.
“两天空气都为良”发生的概率.
【题目】为了整顿道路交通秩序,某地考虑将对行人闯红灯进行处罚.为了更好地了解市民的态度,在普通行人中随机选取了200人进行调查,当不处罚时,有80人会闯红灯,处罚时,得到如表数据:
处罚金额 | 5 | 10 | 15 | 20 |
会闯红灯的人数 | 50 | 40 | 20 | 10 |
若用表中数据所得频率代替概率.
(1)当罚金定为10元时,行人闯红灯的概率会比不进行处罚降低多少?
(2)将选取的200人中会闯红灯的市民分为两类:![]() 类市民在罚金不超过10元时就会改正行为;
类市民在罚金不超过10元时就会改正行为;![]() 类是其他市民.现对
类是其他市民.现对![]() 类与
类与![]() 类市民按分层抽样的方法抽取4人依次进行深度问卷,则前两位均为
类市民按分层抽样的方法抽取4人依次进行深度问卷,则前两位均为![]() 类市民的概率是多少?
类市民的概率是多少?